Paper Walkthrough: DINO
In this post, I'll cover Emerging Properties in Self-Supervised Vision Transformers by Caron et al., which introduces a new self-supervised training framework for vision transformers.

In this post, I'll cover Emerging Properties in Self-Supervised Vision Transformers by Caron et al.[1], which introduces a new self-supervised training framework for vision transformers.
Vision transformers have matured to the point that they now achieve SOTA performance on many computer vision tasks - see my post on CaiT [2] and DeiT [3]. However, there is a depressing amount of semi-supervised pretraining scheme available for them when compared with the richness of the NLP ecosystem. This paper introduces a new self-supervised training methodology, DINO, that attempts to begin filling that gap.
Takeaways
- Based on the inspection of ViT features, it's clear DINO can learn semantic representations from images. Specifically, when examining how the class token attends to the image patch embeddings there are stark features corresponding to scene layout, object boundaries, etc. (see figure from paper below). Related to this point, the authors also find it is beneficial to use smaller image patch sizes than traditionally used in vision transformers, which helps to more clearly resolve these features.
- With no additional fine-tuning or linear classifier, these features are enough to realize SOTA performance in comparison to other semi-supervised image methods.
- Three main concepts, which I'll detail later in the post, allow the framework to function: 1) multi-crop training, 2) centering, and 3) a momentum encoder.

Overall framework
DINO leverages the concept of knowledge distillation, a form of semi-supervised learning. In knowledge distillation a student model is trained to match the output of a teacher model. Typically, this is done in a supervised setting where the teacher model is a strong teacher, meaning it has been trained on labeled data. However, we don't have any ground truth labels, as this is a semi-supervised learning task, so instead in this framework the teacher learns the student via an update from the student networks parameters. I'll walk through the details in later sections, but below is the overall setup of DINO.
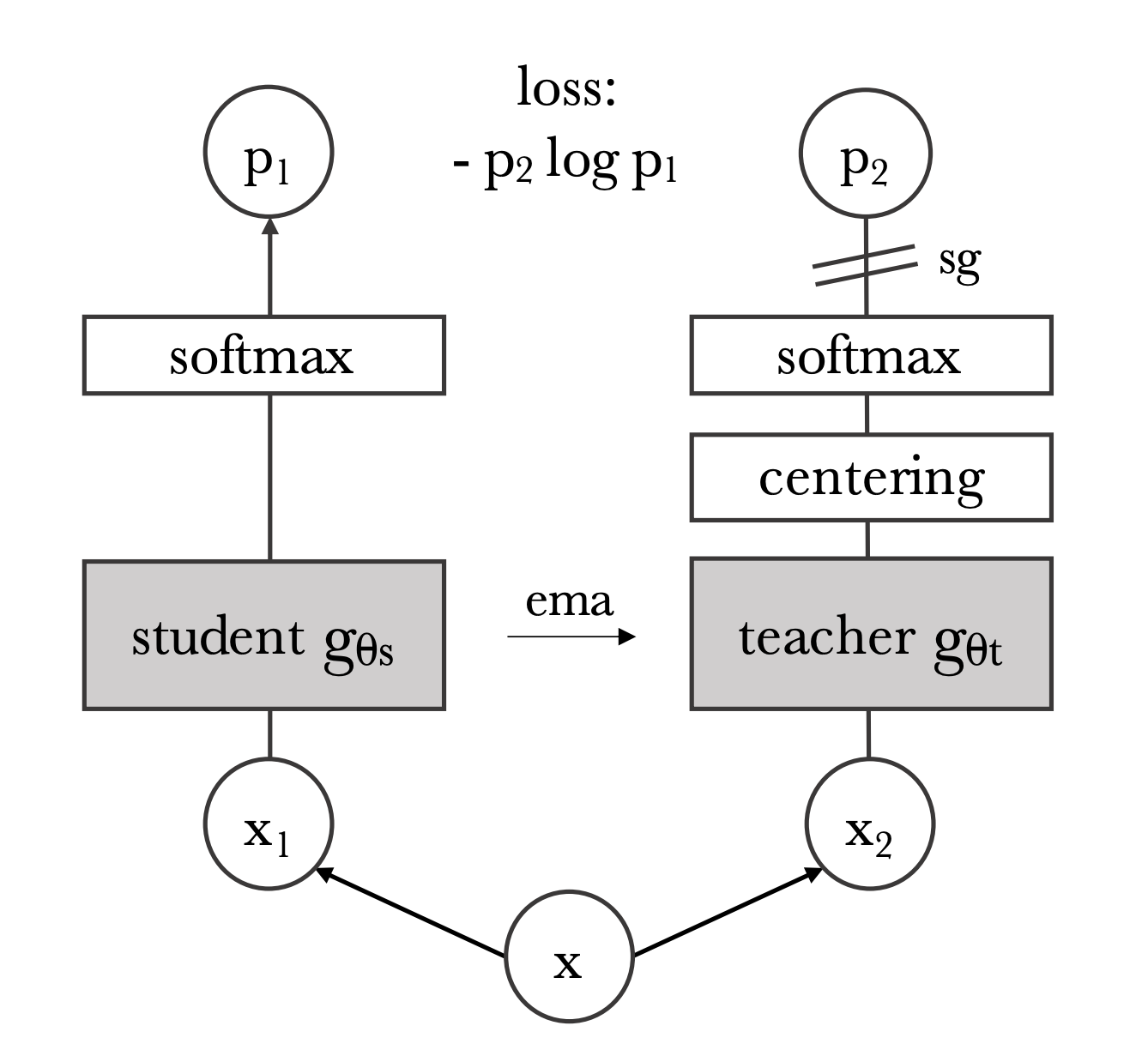
I'll start with the inputs:
1) Input generation
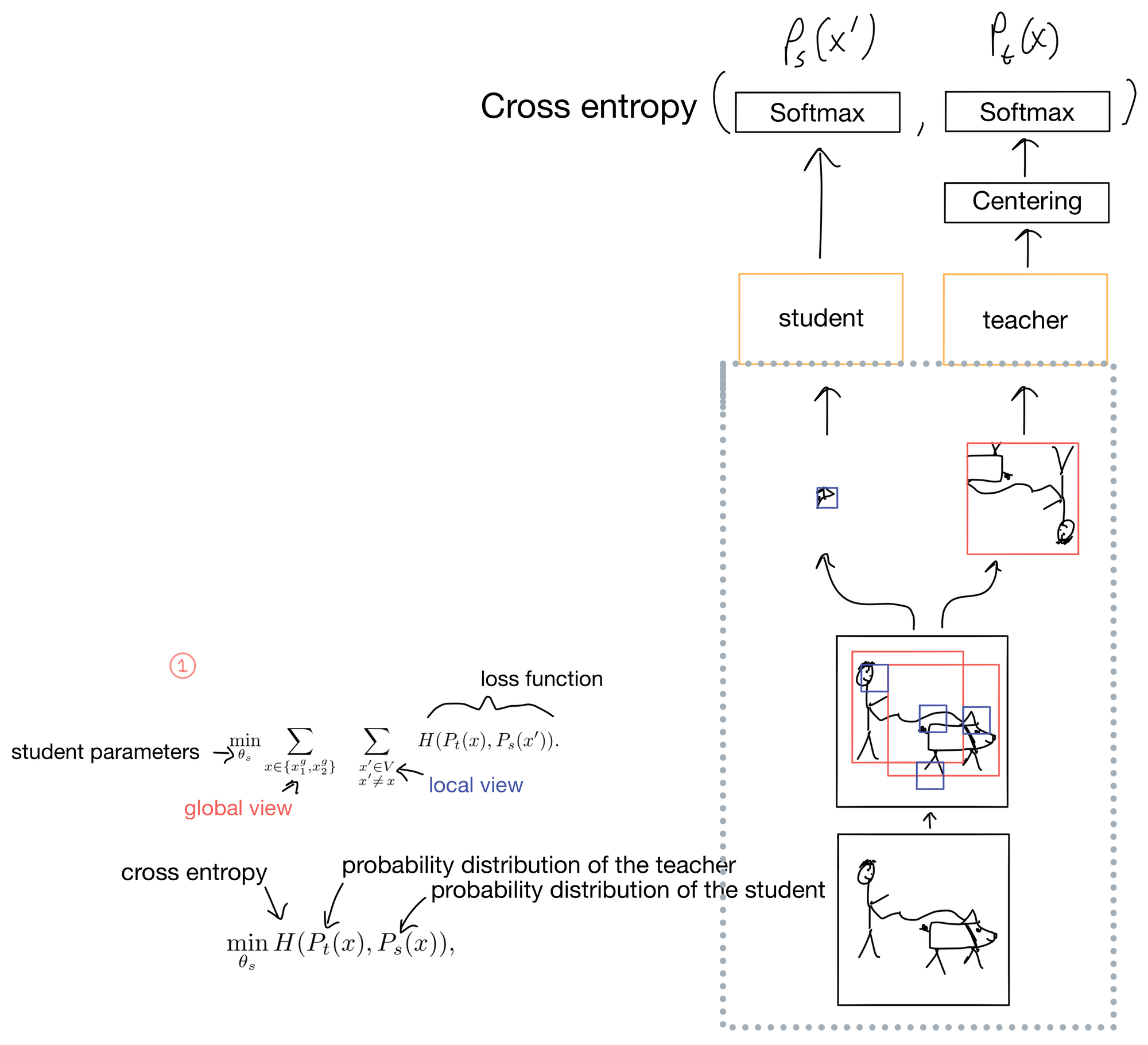
Conceptually, the reason DINO works is because it projects two different augmented "crops" of the same picture, and tries to predict that these two crops are of the same class. Remember since this is a semi-supervised learning task we don't actually know what the classes are, so the number of potential classes is a model hyperparameter.
First an image is passed through two different random augmentation/transforms (Fig 1). The resulting two images are cropped into two different types of views: a local view covering <50% of the image (shown in blue), and a global view covering >50% of the image (shown in red). The teacher only ever get's the global crops, while the student can get either the local or the global crop of the separate image that is augmented differently than the teacher's image. This prompts the network to learn “local-to-global” correspondences in the image.
2) Centering and Sharpening
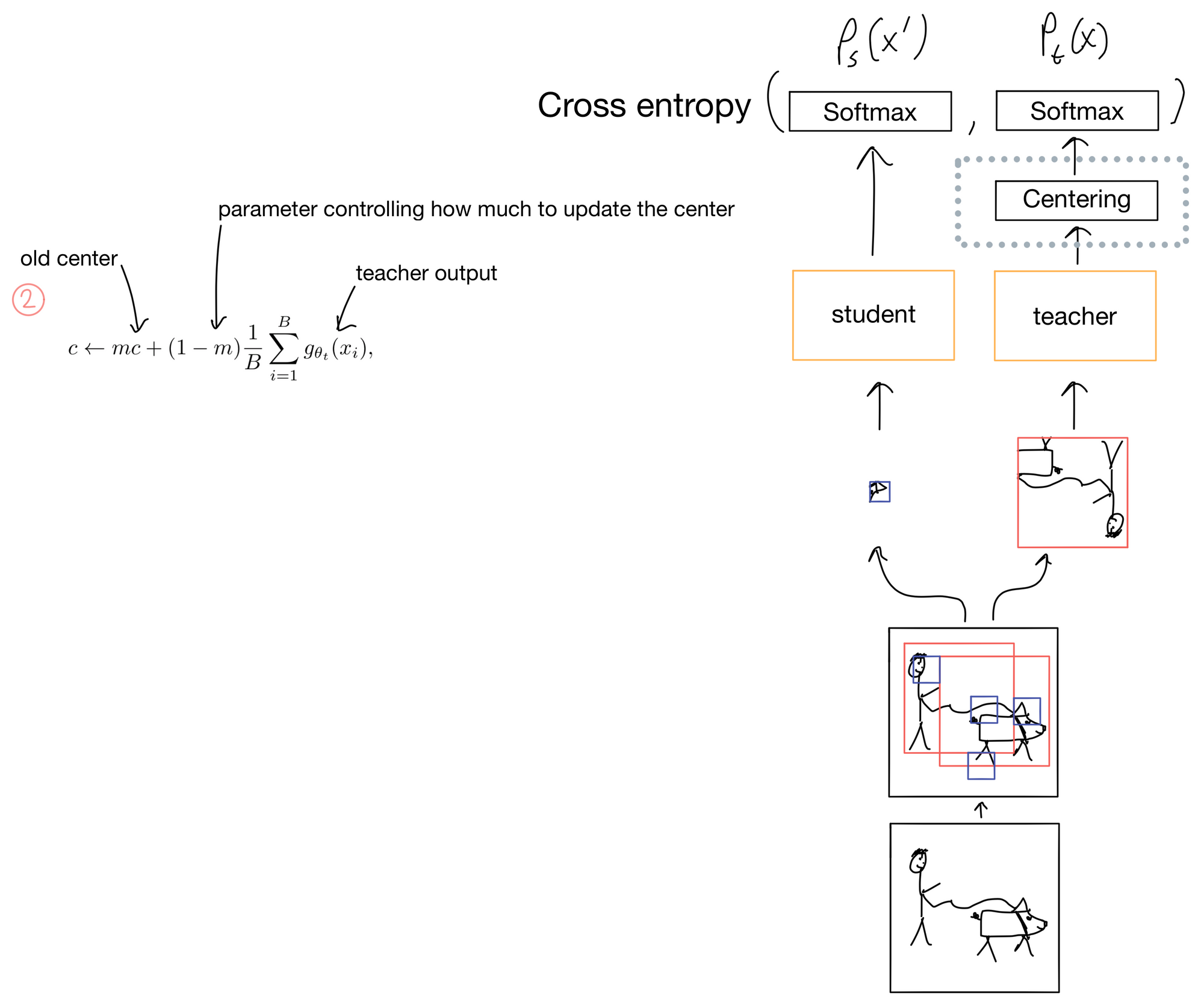
The key regularization step in DINO is the centering/sharpening of the teacher outputs. Without these steps mode collapse becomes an issue, and the probability distribution of the teacher will either completely flatten or excessively sharpen. To address this DINO applies a centering step (Fig 2) where a center c is added to the teacher distribution. This has the effect of flattening the distribution (similar to label smoothing), while in the next layer, the softmax function, has a temperature parameter that controls how sharp the output probabilities of the softmax are (Fig 3). The student also has this temperature parameter but it is set separately from the teacher and does not sharpen the output to the same degree.
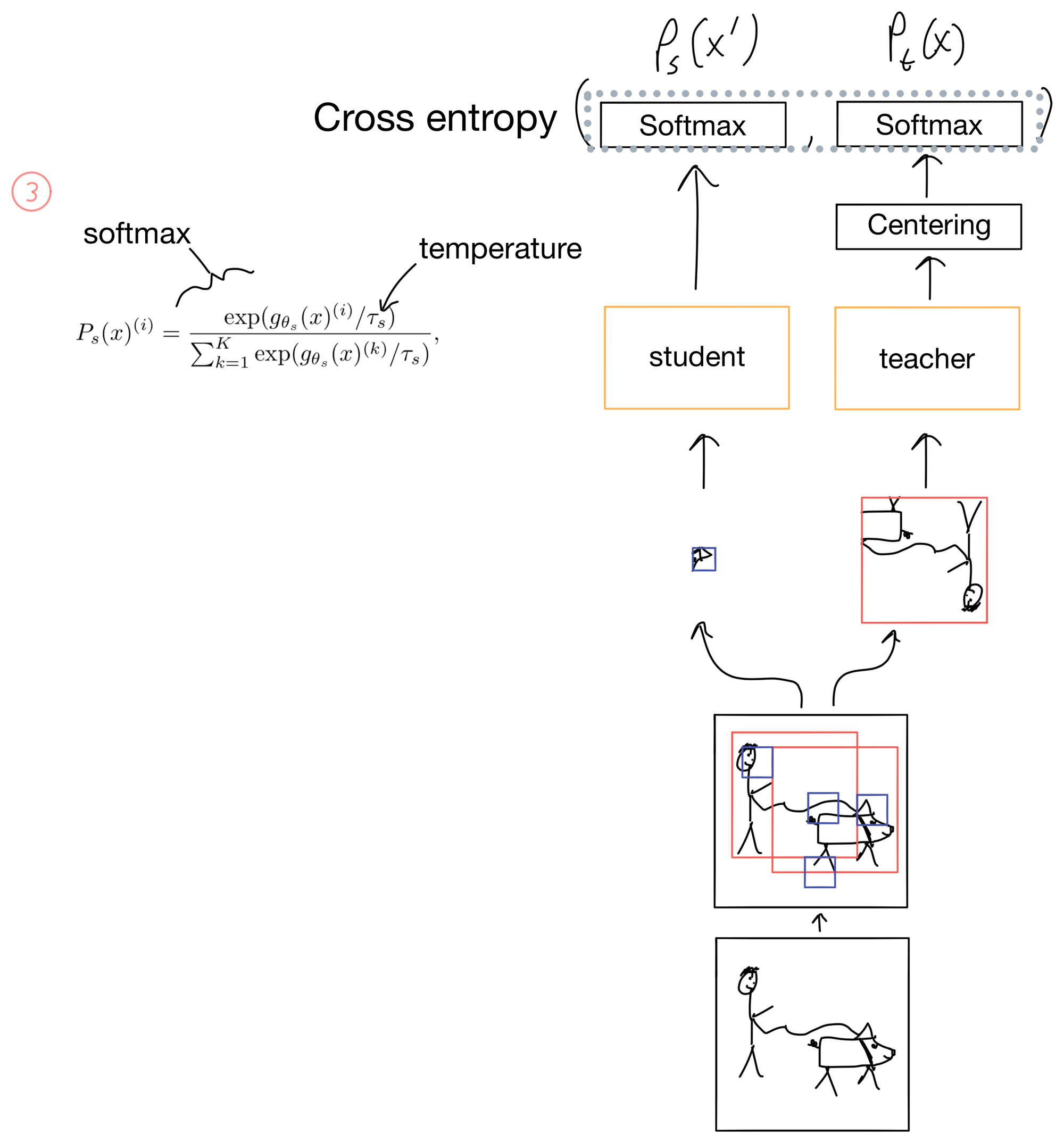
Following normalization with softmax, the student distribution is matched against the teacher distribution using a cross entropy loss function.
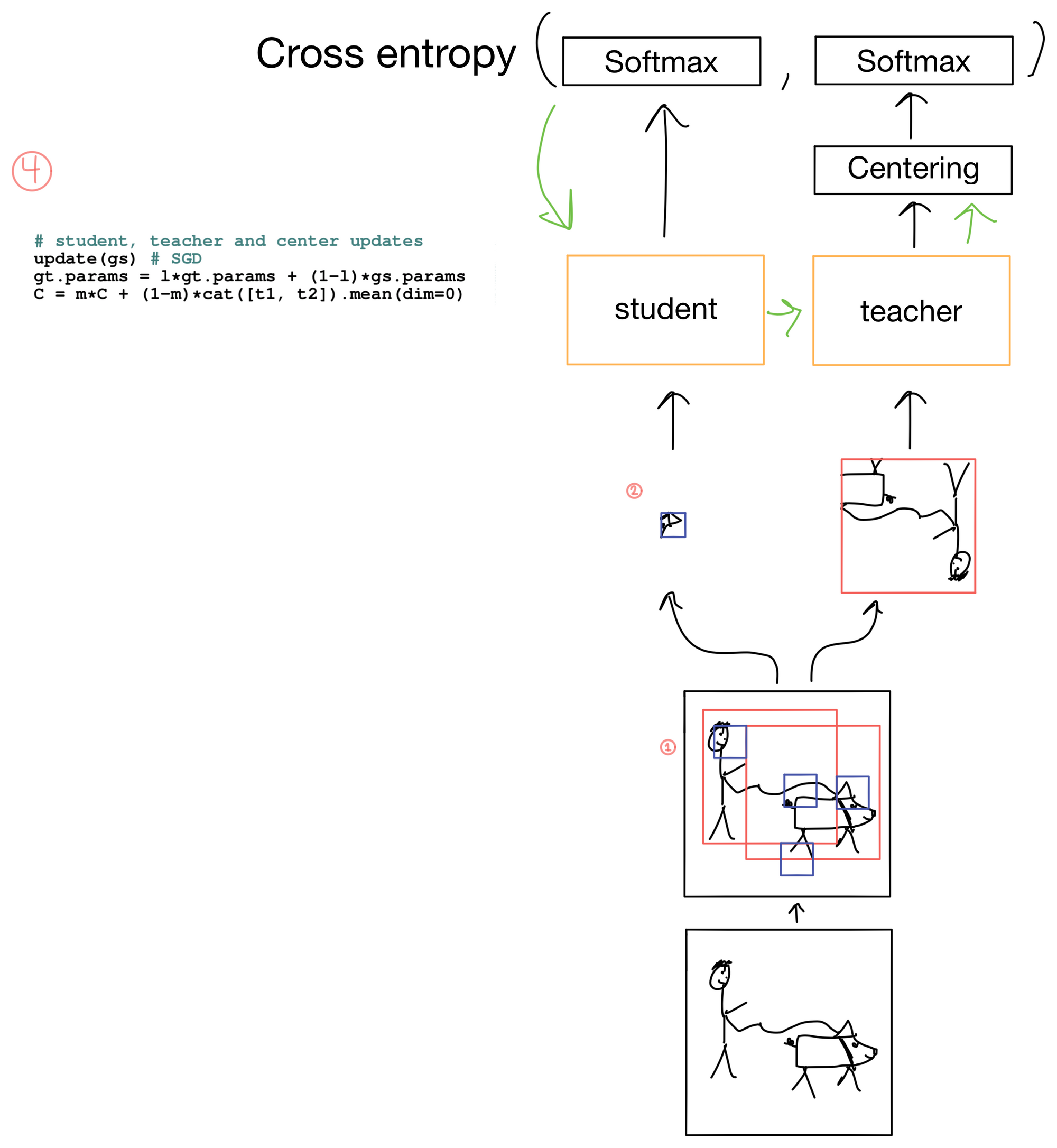
3) Updating the DINO
Now that we have our loss, we can update the network (Fig 4). The loss is only used to update the student parameters. It is not used to update the teacher parameters. After the student parameters are updated, an exponential moving average (EMA) of the student parameters are used to update the teacher parameters. The EMA prevents the teacher parameters from updating too quickly. After parameter updates the teacher also gets a new centering parameter.
Cheers :). Hope you found the post helpful!
1. DINO: https://arxiv.org/abs/2104.14294
2. CaiT: https://arxiv.org/abs/2103.17239
3. DeiT: https://arxiv.org/abs/2012.12877
