Paper Walkthrough: Cross-Covariance Image Transformers (XCiT)

XCiT^[1], from El-Nouby et al., is another in a long line of modifications to the Transformers architecture  originally proposed by Vaswani et al.^[2]  Transformers have demonstrated extreme flexibility in a variety of tasks due to their ability to route information between input tokens in a sequence. However, in multihead self-attention (MSA), the attention matrix always has number of columns and rows equal to the length of the input sequence. Meaning that memory and time complexity scales with O(n²) asymptotics, which makes it challenging to use long sequence lengths (> ~1000 tokens) with the Transformer architecture. Recently, much effort has been directed to reducing this quadratic complexity in the number of input tokens to a linear complexity. Previous methods have also attempted this feat, see the Nyströmformer^[3], for example. XCiT attempts to reduce this quadratic complexity by mixing information between channels rather than tokens in the input sequence. More on exactly what that entails later in the post.

XCiT

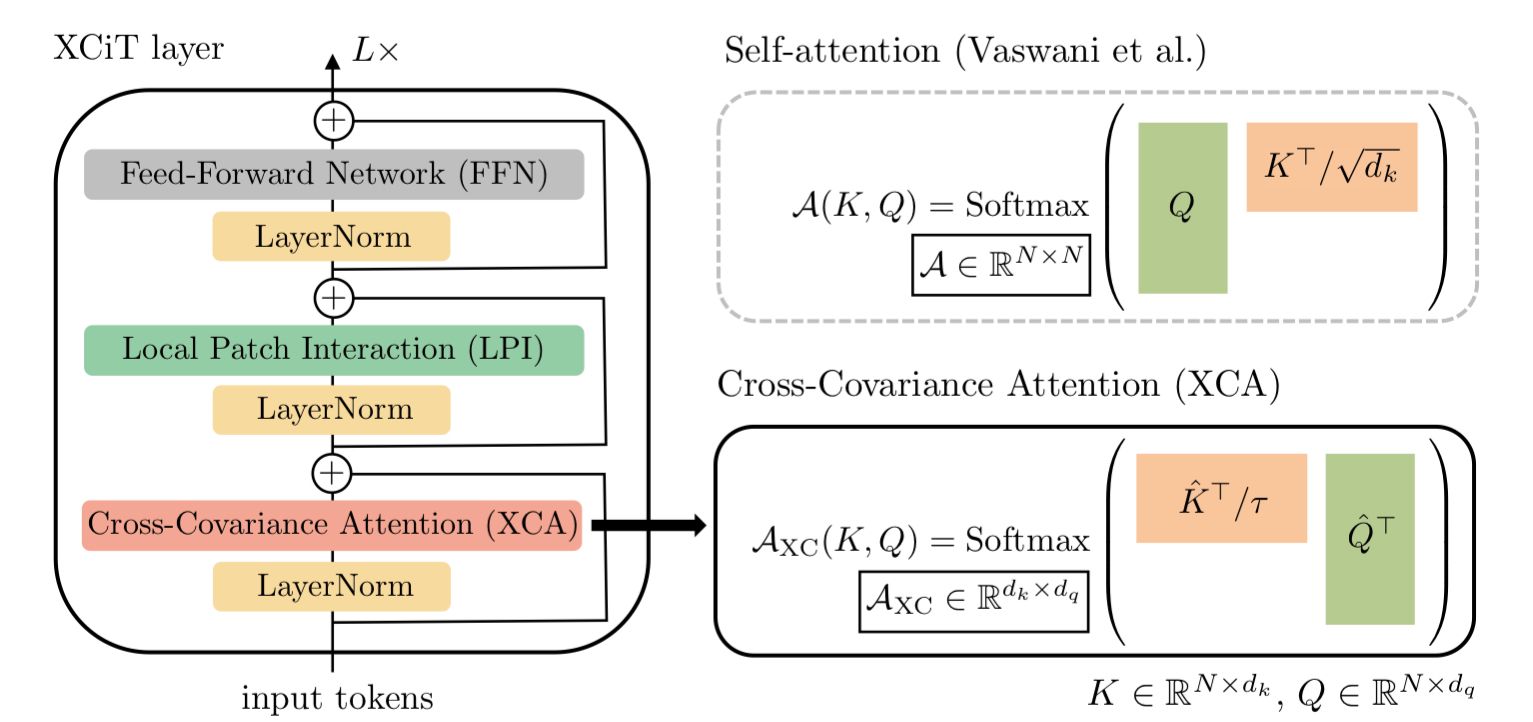
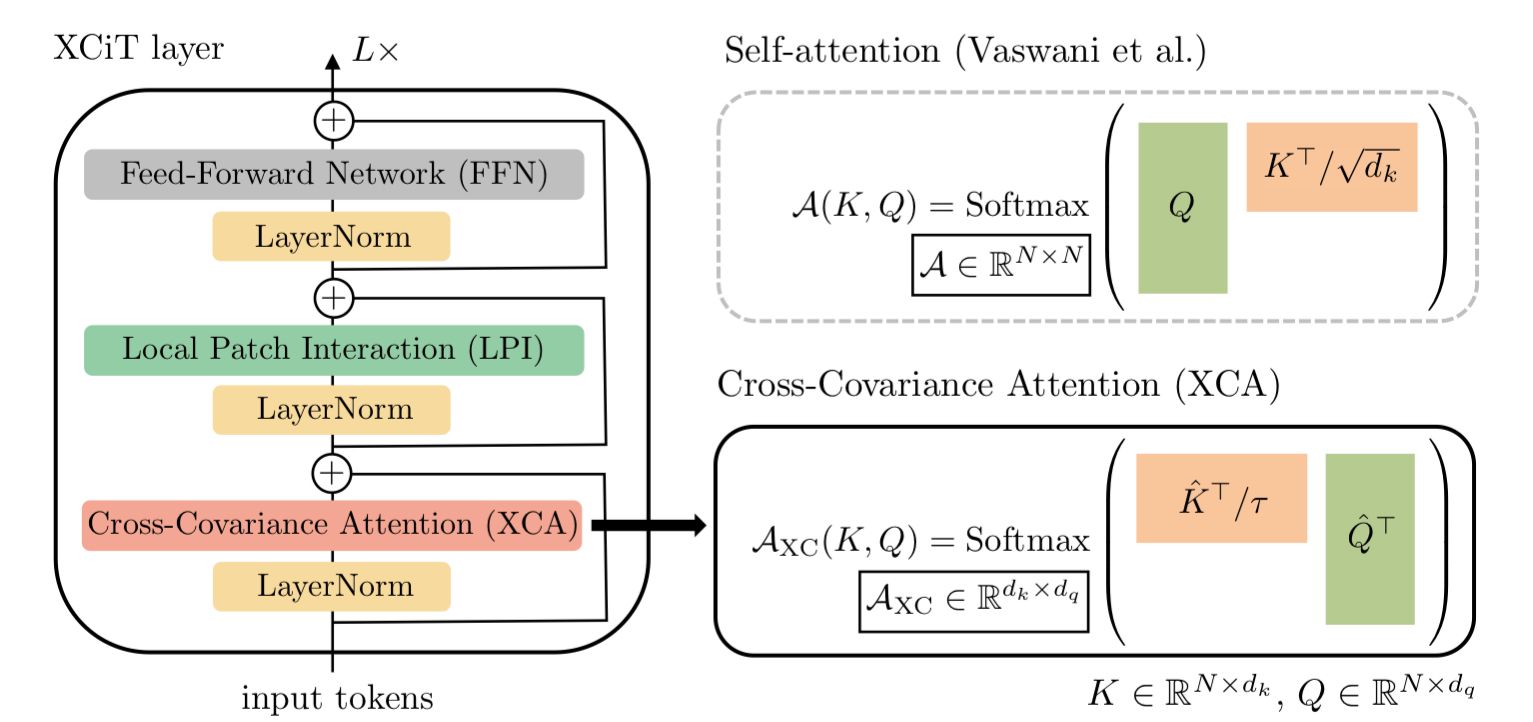
The key differences in XCiT, when compared to a traditional transformer, are 1) the replacement of the self-attention layer with a Cross-Covariance Attention (XCA) layer, and 2) the addition of a Local Path Interaction (LPI) layer.

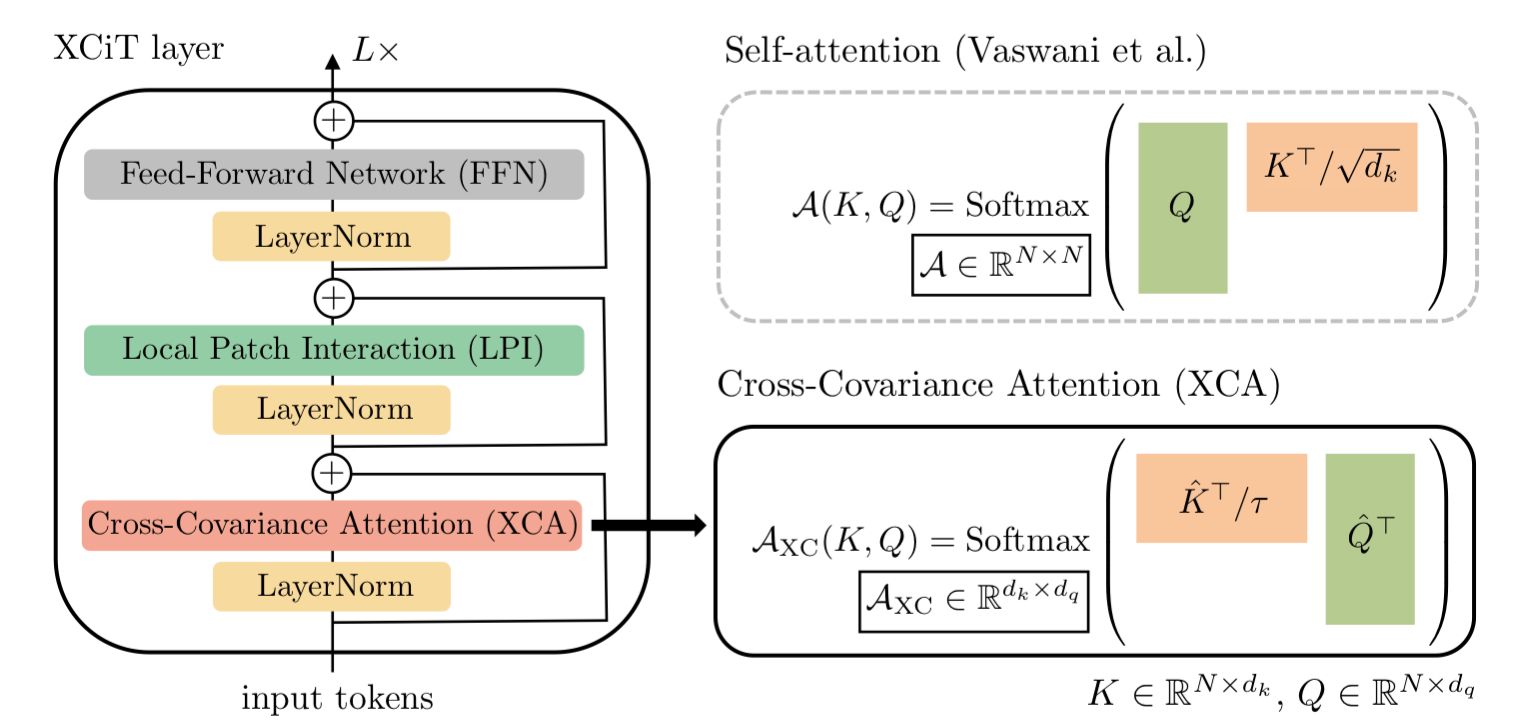
Cross-Covariance Attention (XCA) layer

We'll start with the XCA layer. This layer is actually remarkably similar to a vanilla self-attention layer, but with two key differences: 1) the key matrix in the attention operation is transposed, and 2) the addition of a learned temperature parameter T that scales the keys.

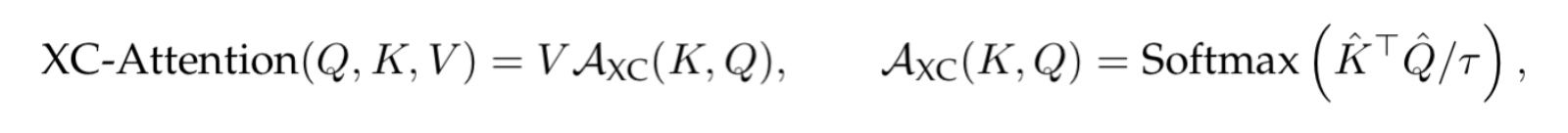
Why does this result in a linear complexity in memory and compute? To make this clear, let's look at the matrix operations involved in the two methods a little more closely. We start with vanilla self-attention below.

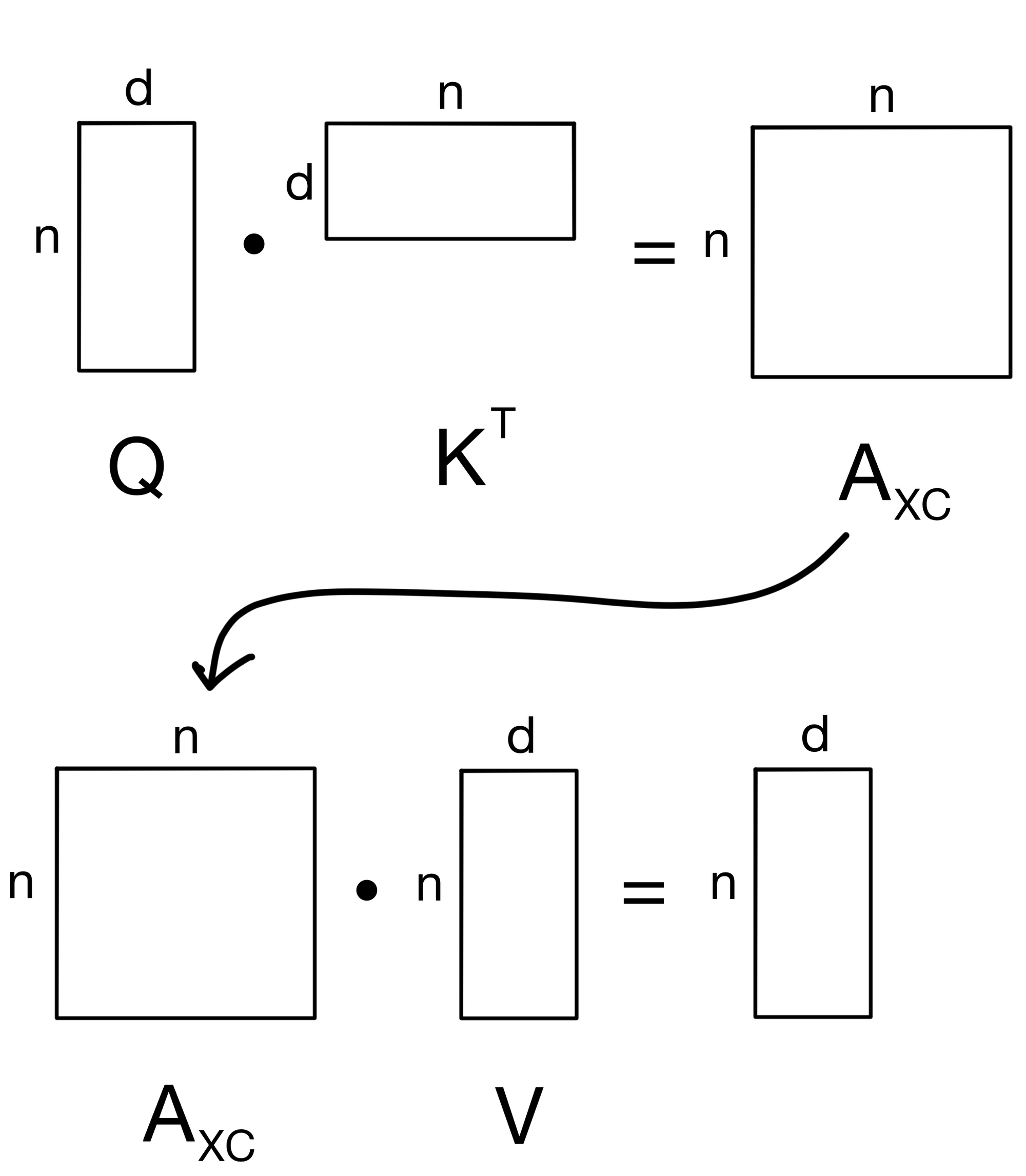
Note that the attention matrix (A_XC) is n x n. Where n is the number of tokens in the sequence and d is the number of features (i.e. channels).

In contrast, if we look at the XCA attention operation:

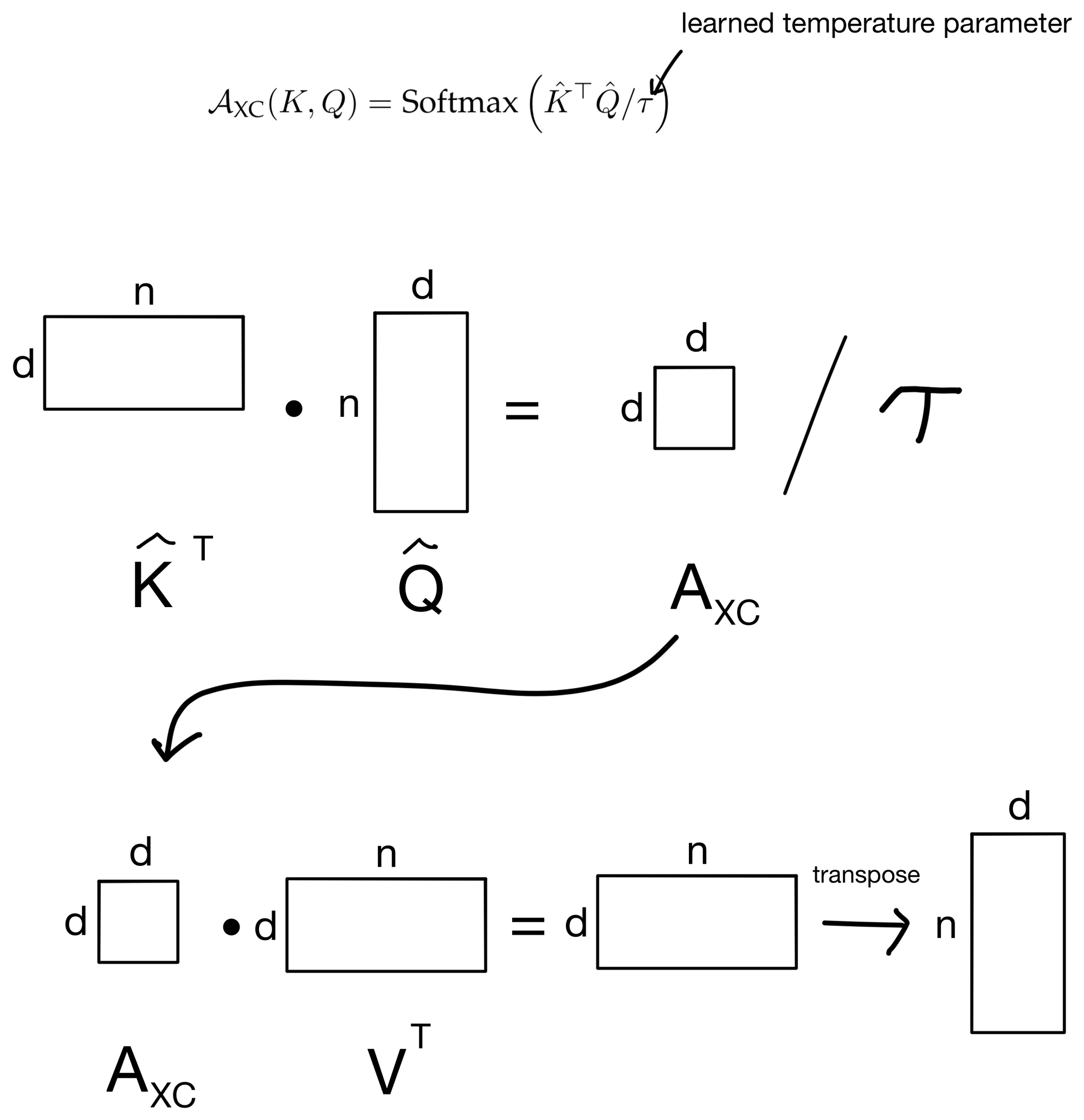
We see that the attention matrix A_XC is a d x d matrix, so instead of being quadratic in the number of tokens we are actually quadratic in the number of features/channels, which is more ideal since we can keep the number of channels constant while increasing sequence length to our hearts content. Hence, this is why XCiT allows for the use of longer sequence lengths. Additionally, we can see why the layer is called the cross-covariance attention layer, as we are quite literally taking the covariance between the features of the key and query matrices.

Local Patch Interaction (LPI) layer

So that is the XCA attention layer, let's move on to the second major addition on the Transformer architecture: the addition of the LPI layer.

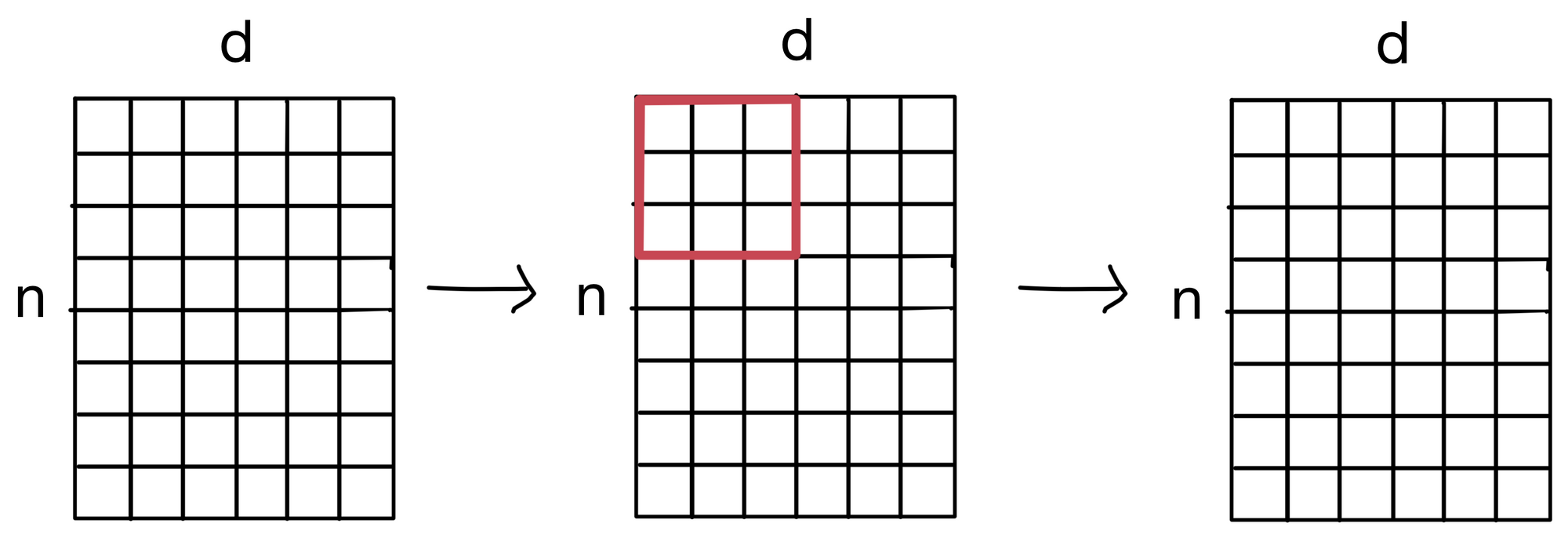
The LPI layer is necessary because we need a way to mix information between tokens in the input sequence. In traditional self-attention, this is done via the attention mechanism in the attention layer. But with the XCA attention layer, information is mixed between the channels, not sequence tokens. So we need an alternative way to spread information between the tokens, this is where LPI layer comes in.

LPI is a fairly simple layer. All we do is apply a 2D convolution across the the layer input (which is the n by d matrix that is eventually projected to the keys, queries, and values for the attention layer). By applying this convolution, it allows the tokens to mix information among themselves, albeit at only between neighboring tokens in a given layer. However, the more layers we propagate through, the larger the receptive field of the convolution becomes. Eventually resulting the the sharing of information between all tokens (assuming the stack of encoder layers is deep enough).

Visualizing Attention

The addition of the XCA layer also begs the question, how can we visualize how the tokens are attending to each other if they are not involved in the attention layer? The simple answer is, well, we can't. However, we can still see how the class (CLS) token, which is typically used for whichever task the model is trained for, attends to each input token. To do this, XCiT incorporates Class-Attention layers that were originally introduced in CaiT^[4].

In class attention layers, the class token is not passed into the network initially with the rest of the input token embeddings, but instead only in the final few layers.

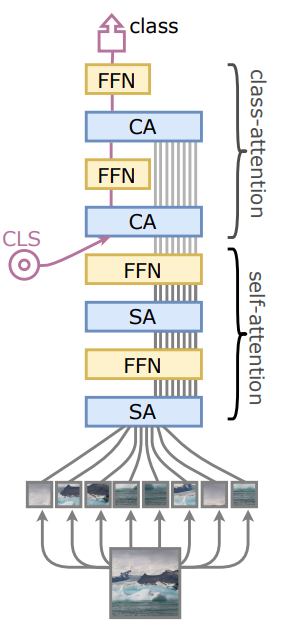
Additionally, the tokens are also not permitted to attend to each other, avoiding the quadratic complexity that XCiT is trying to avoid in the first place. Below the matrix operations in class attention layer are visualized.

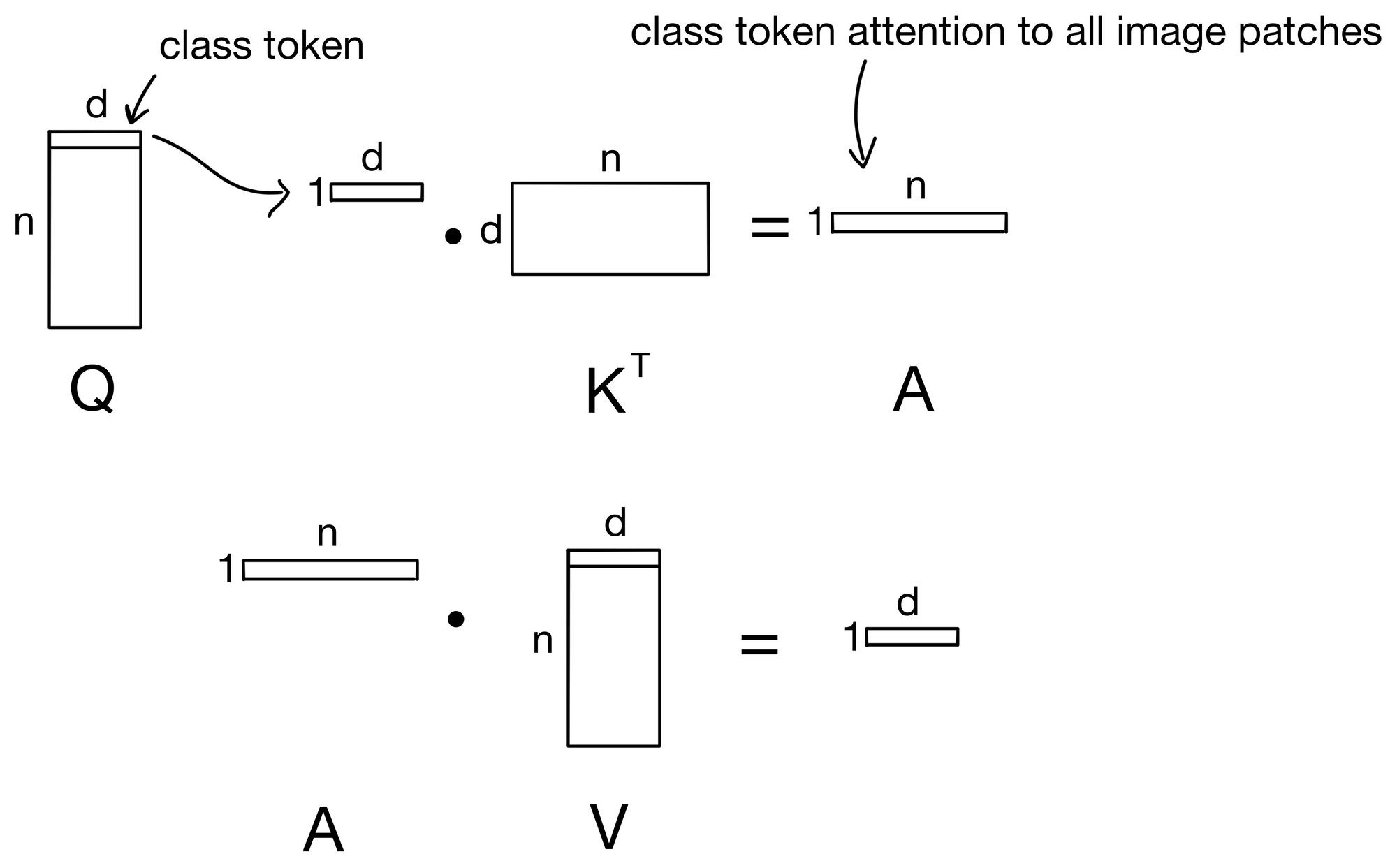
You'll see that we can still avoid the quadratic complexity since we don't need every token to attend to every other token, but instead only allow the class token to attend to each token.

Hope you enjoyed the post :)

1. XCiT: https://arxiv.org/abs/2106.09681
2. Attention Is All You Need: https://arxiv.org/abs/1706.03762
3. Nystromformer: https://arxiv.org/abs/2102.03902
4. CaiT: https://arxiv.org/pdf/2103.17239.pdf