Paper Walkthrough: Attention Is All You Need
In this post I walk through the classic paper Attention Is All You Need

Introduction
In this post I’ll be covering the classic paper Attention Is All You Need [1]. At the time of publication in 2017, top performing models for sequence-based tasks were recurrent or convolutional neural nets that made use of attention mechanisms to route information between model encoder and decoder. Attention Is All You Need instead showed that you can skip the recurrence and convolutions by using an attention only architecture, which they dub the Transformer. Since the paper's publication, attention-centric models have become dominant in the field of NLP, and have even recently started to show impressive results in imaging tasks (see ViT [2]).
I focus more on the code/matrix operations than the overall reasoning of the paper. For a good overview of transformers check out Yannic Kilcher's Youtube video. I’ll be using this repository from by jadore801120 that is a pytorch implementation of the original paper repository. I’ll go through the code from the ground up, starting with attention, and incrementally build up the Transformer architecture.
Note: When running through matrix multiplications I will typically ignore the first dimension (batch dimension) for simplicity sake.
Scaled Dot-Product Attention
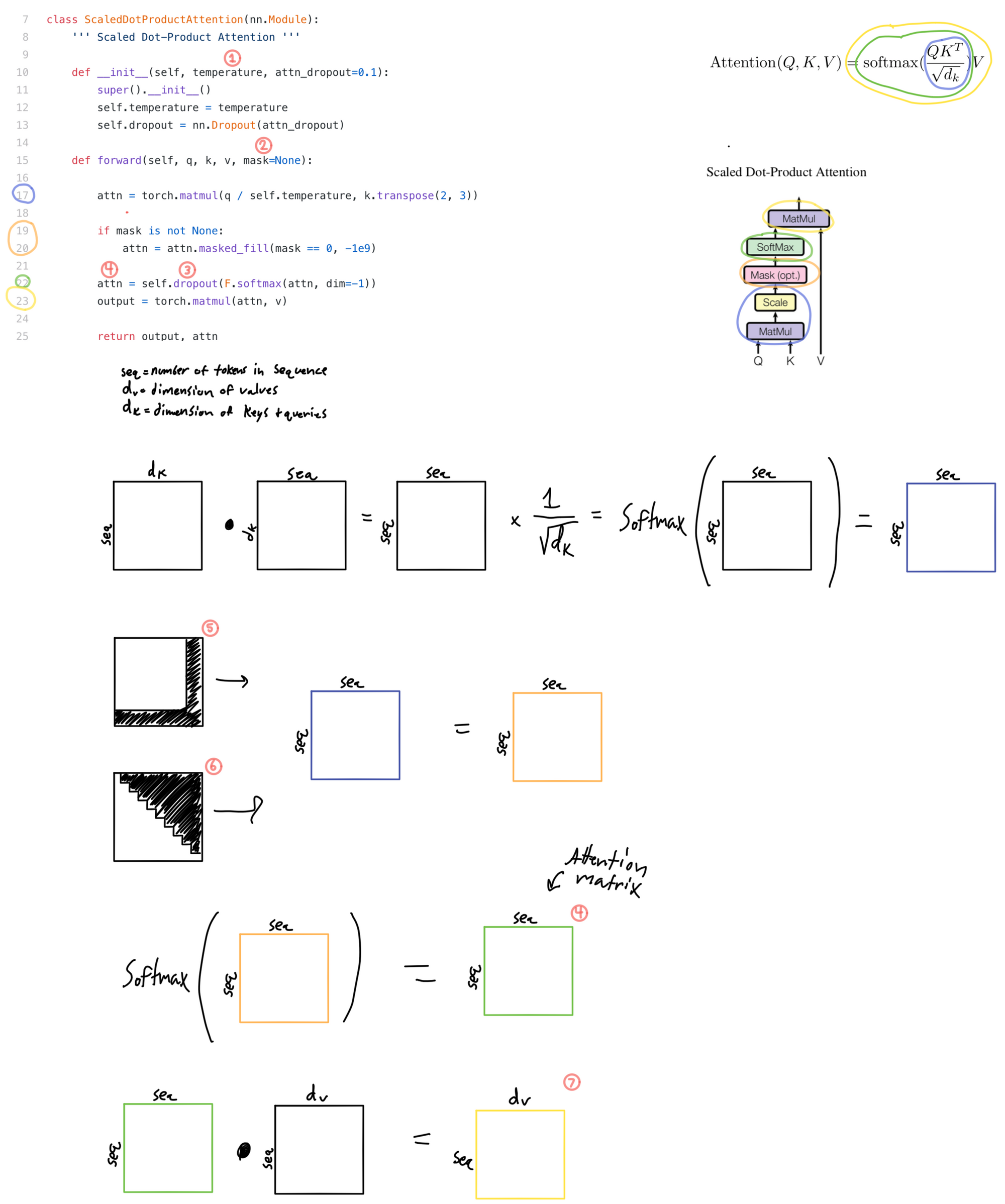
- The scale term is called temperature in the code, i.e.
temperature= 1/sqrt(dk ). - The mask is used to A) mask out the attention matrix for <pad> tokens in the sequence and B) mask out the attention matrix in the second multihead attention in the decoder so tokens after the token being predicted are zeroed out so the mechanism can't "look ahead" in the sequence.
- This dropout layer isn't mentioned anywhere in the text (that I could find anyways), so useful to know it's in there. This also may not bee in the original paper code repository as what I'm annotating here is not the official repository.
- The result of the first matrix multiplication, masking, and softmax is known as the attention matrix. The values in this matrix show how much each token in the sequence is attending to other tokens.
- The <pad> tokens need to be masked out
- Mask for second multihead attention to prevent looking ahead in the sequence (this mask is not necessary for self attention).
- The output of the attention mechanism. This can be loosely thought of as important information about the tokens in the sequence, which is the result of information being routed via attention.
Multi-Head Attention
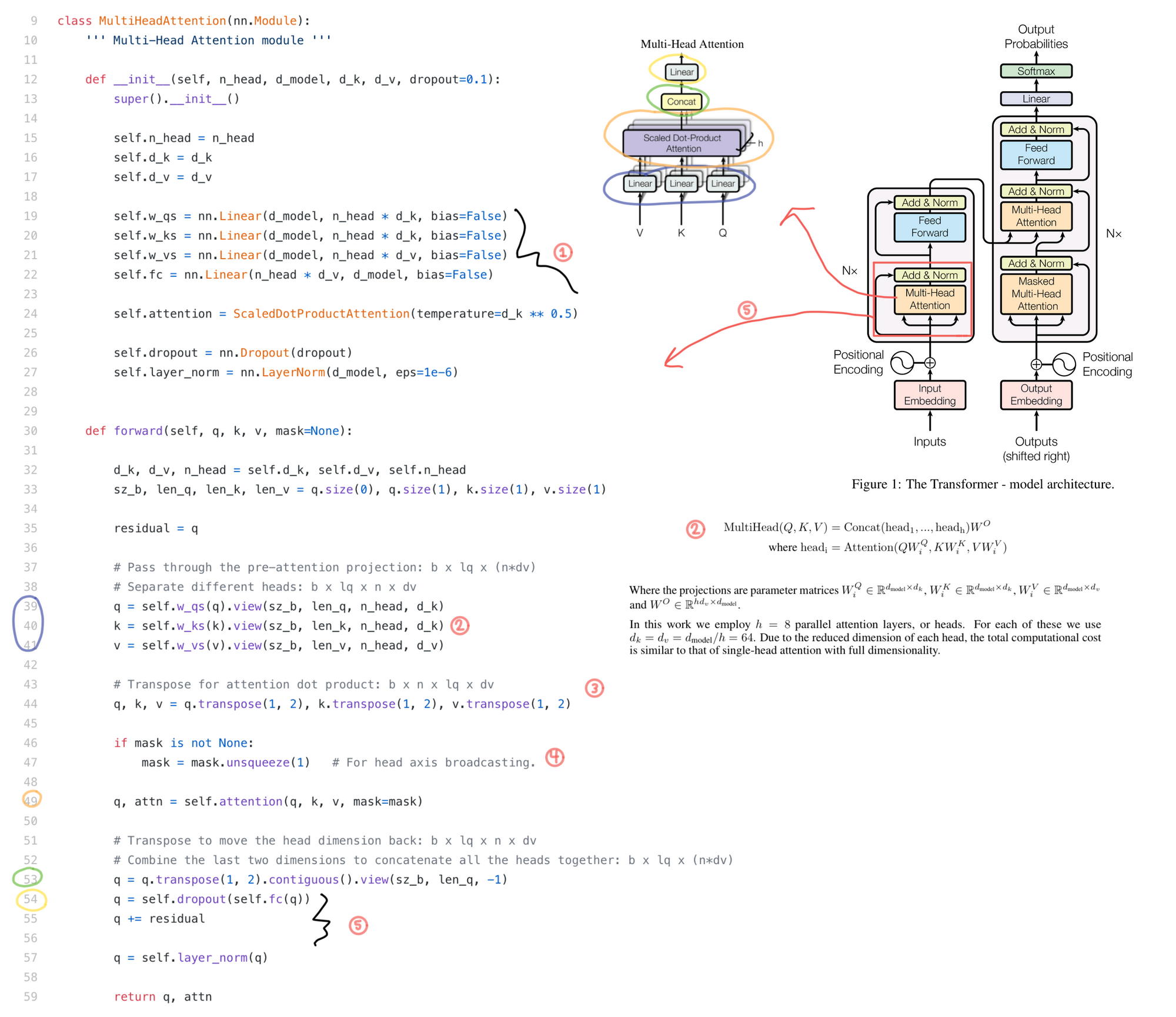
- Initializing the linear layers and the scaled dot product attention discussed in the previous section
- Q, K, and V need to be reshaped after the linear layer to add a head dimension so they can be input into the multihead attention.
- Q, K, and V also need to swap the head and sequence (lq in the code) dimension so the last two dimensions (2 and 3) are sequence and dmodel / h
- Adding a head dimension to the mask.
- Transformations that finish off the multihead attention sublayer. They are applied after concatenation of the outputs for each attention head.
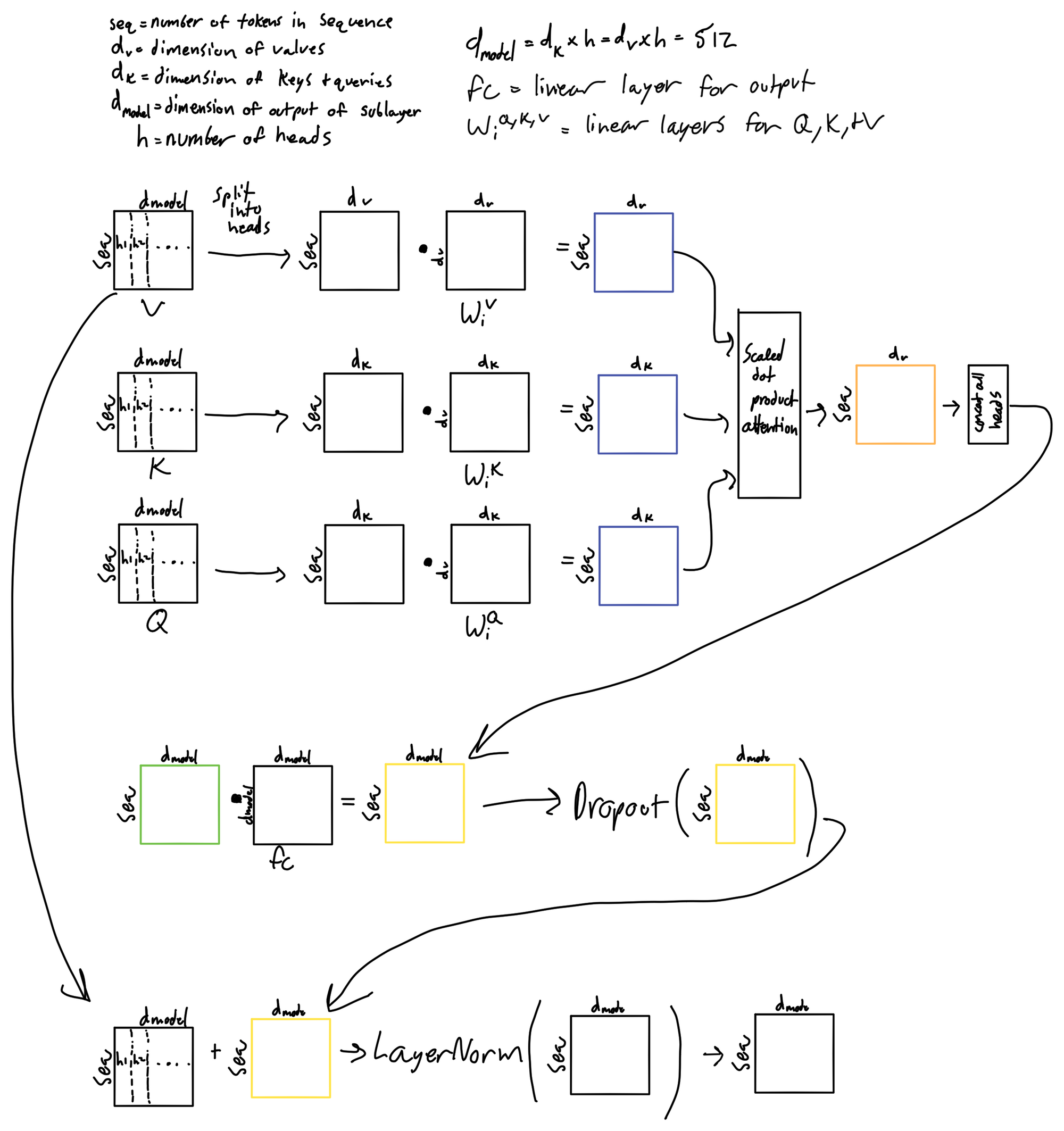
Below is a walkthrough of the matrix operations in the layer
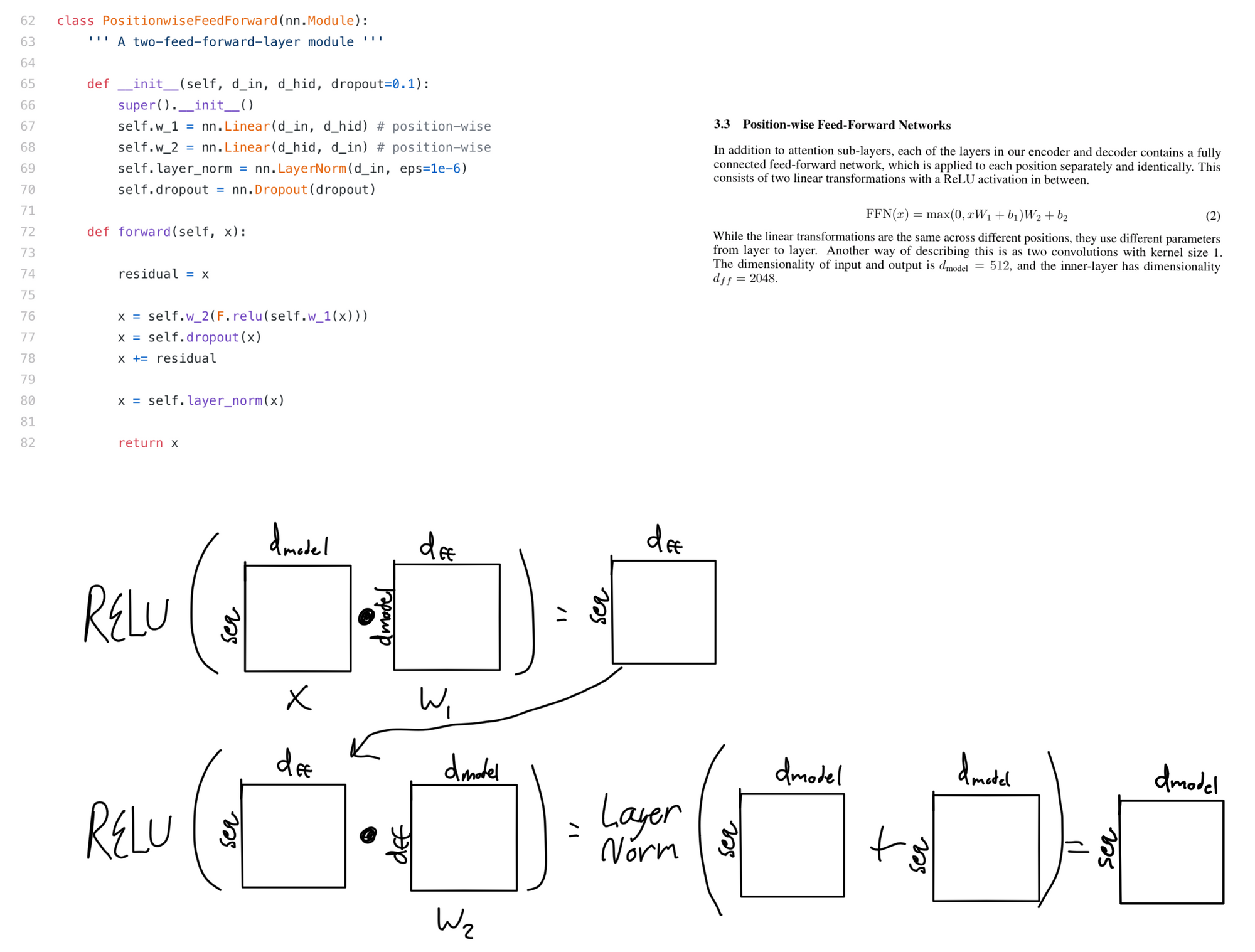
Position-wise Feed Forward Sublayer
The feed forward sublayer is fairly straightforward. It is two linear layers followed by dropout, addition of the residual input, and layer normalization. If you work through the matrix algebra this ends up being equivalent to doing two convolutions with a size of 1x1 and dmodel or dff filters.
The Transformer Architecture
Putting it all together into the Transformer architecture...
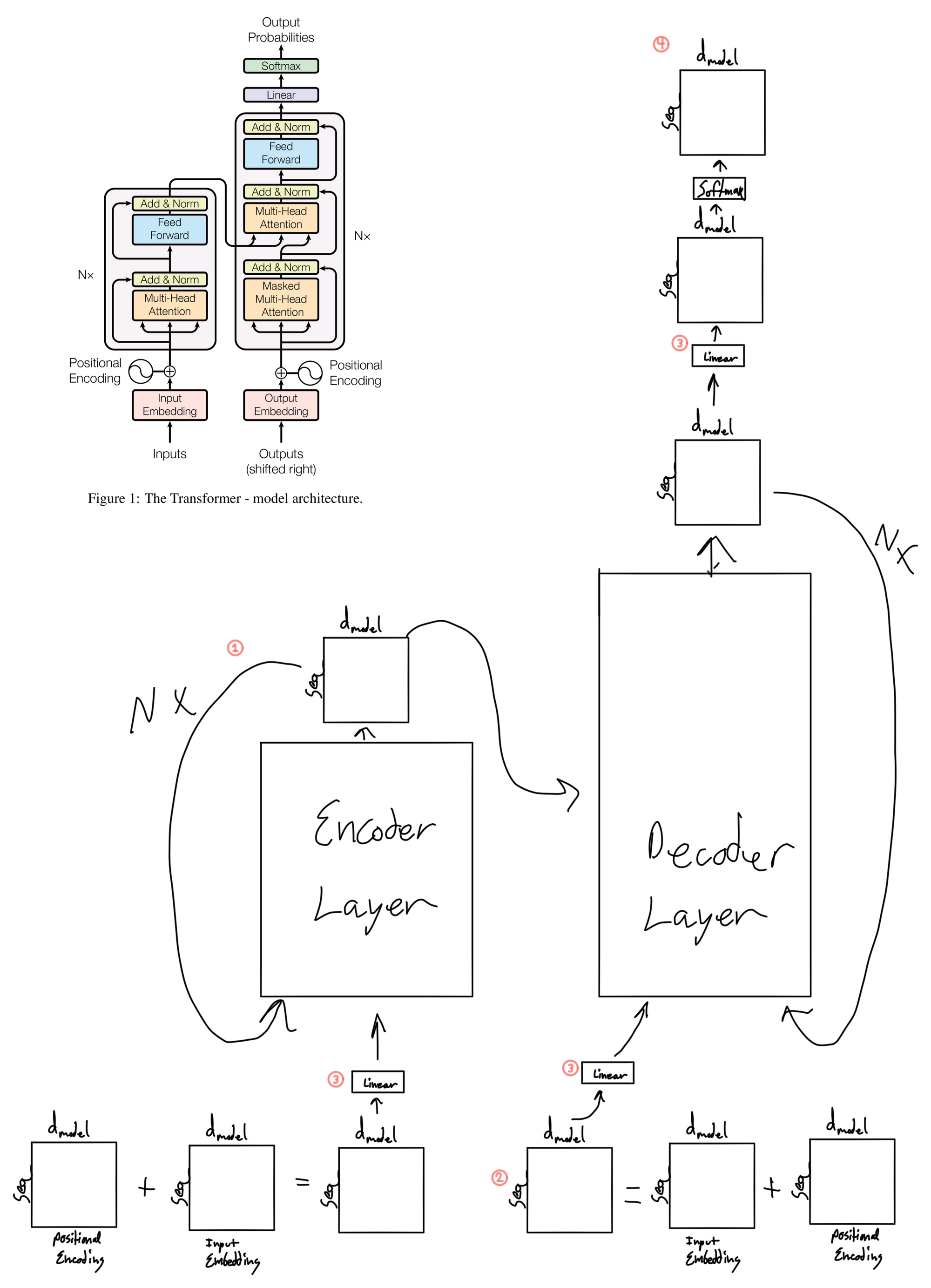
- There are N=6 total encoder layers and N=6 total decoder layers. The output of each layer is used as the input to the next layer until it reach the last layer, in which case it is either passed into the decoder (in the case of the encoder) or passed into the output linear layer and softmax (in the case of the decoder).
- This matrix represents the sequence to be produced for whatever task the model is performing (translation in the case of the paper). The first tokens in the sequence will be words that have been translated so far, as the model is applied in an autoregressive fashion.
- The linear layer for the input and output word embeddings is shared. It is also shared with the very last linear layer in the model prior to output. This is commonly done in language modeling and is done because of the similarity in tokens between the input tokens and target tokens. For example, English and latin languages share an alphabet so token representations may be similar. However this may not be the case for something like English to Chinese translation. In that case it may not be a good idea to share weights between these layers.
Footnotes
1. https://arxiv.org/abs/1706.03762
2. https://arxiv.org/abs/2010.11929
