Paper Walkthrough: A Neural Algorithm of Artistic Style

In today's post I'll discuss neural style transfer as implemented by Gatys et al. ^[1], which introduced one of the first deep learning methods for neural style transfer. As we know humans are good at, well, creating art. At the time of paper publication in 2015, there weren't any well performing methods to transfer the style of an image to the content of another image. The paper introduces the first method to actually do the above by producing credible stylized images.

So how's it all work?

Overall Setup

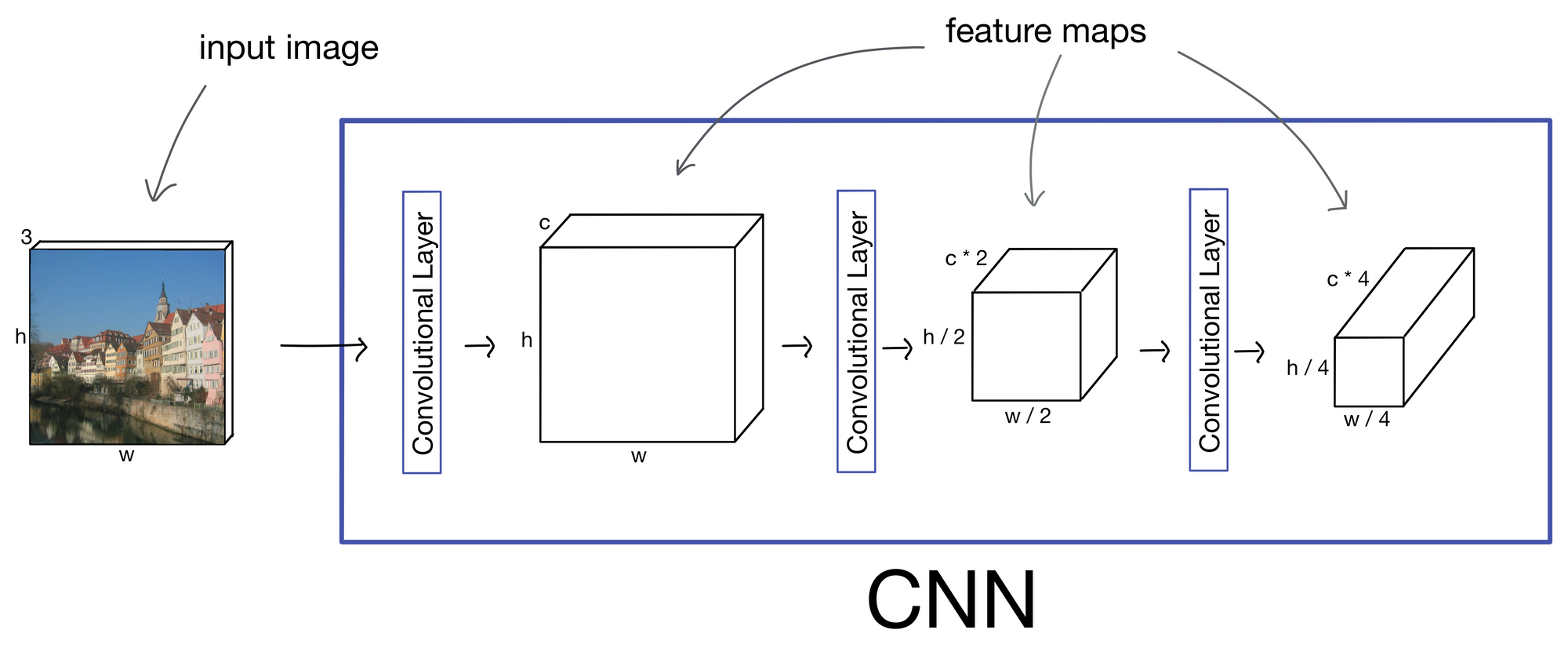
The authors' style transfer method uses the convolutional neural network (CNN) VGG ^[2] as a base. In CNNs, each convolutional layer will output a set of activations known as a feature maps (for a more in depth explanation of CNNs see my post here). More on how later in the post, but these feature maps are ultimately what the method leverages to generate the output stylized image.

First, a quick note. In the schematics for this post I represent VGG in simplified form as a basic three layer CNN for the sake of visual simplicity. In the actual VGG architecture, the operations shown below are done after each max pooling operation following a block of convolutional layers.

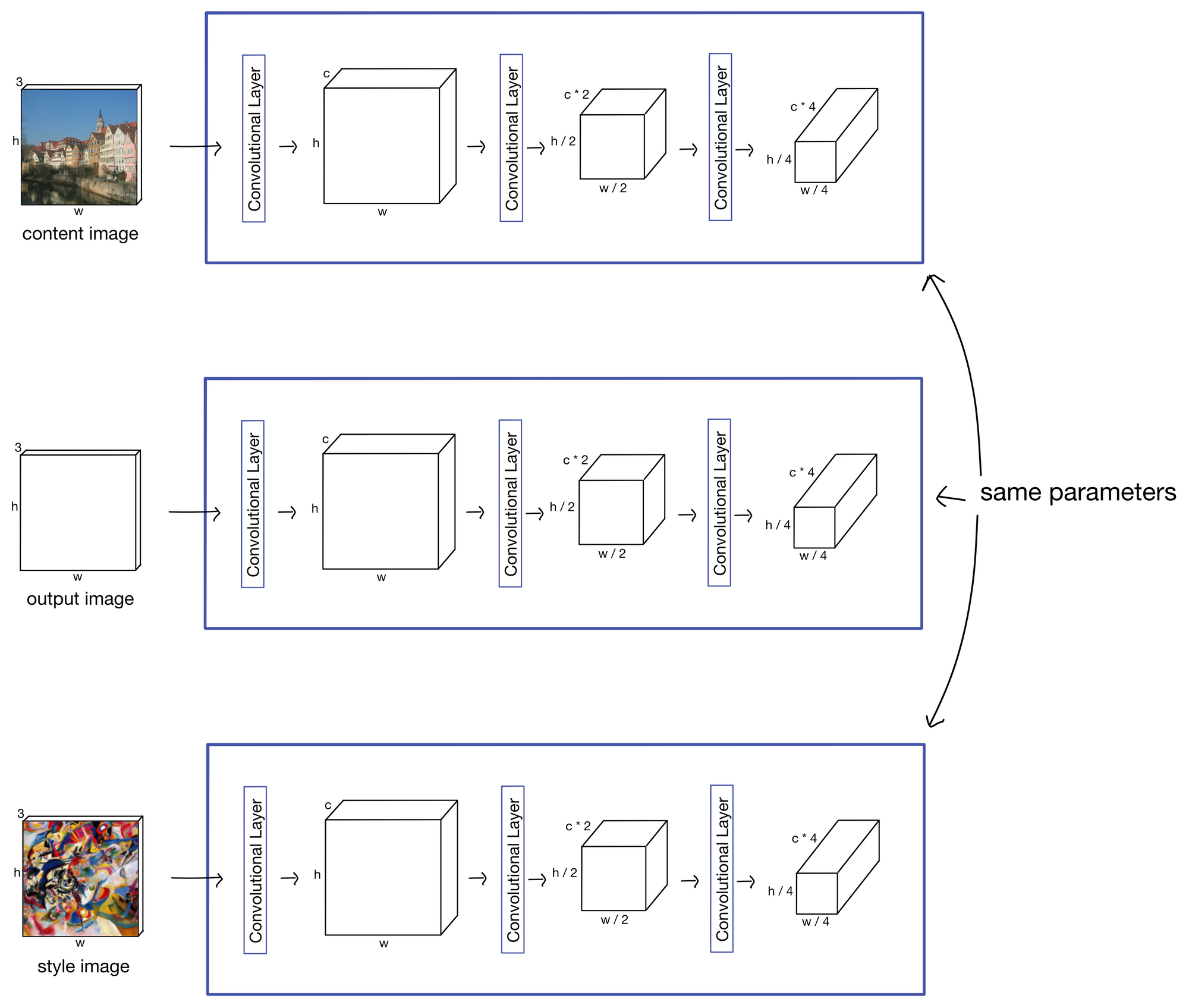
To create the stylized image, the network is fit jointly to three different input images. The first is the content image. This image has the content we want our final stylized image to contain. Second is the style image, which displays the style the output image should contain. And the third is the output stylized image itself, which is a trainable set of parameters. At the start of training, the stylized image is initialized as white noise, and becomes progressively more stylized during as the network is fit.

There are two main loss functions in the network that are combined and optimized to produce the stylized output image: the content loss and style loss.

Content Loss

The purpose of the content loss is to ensure the stylized output image represents the content of the content image. The content loss is calculated from the feature maps produced by the content image and the stylized output image.

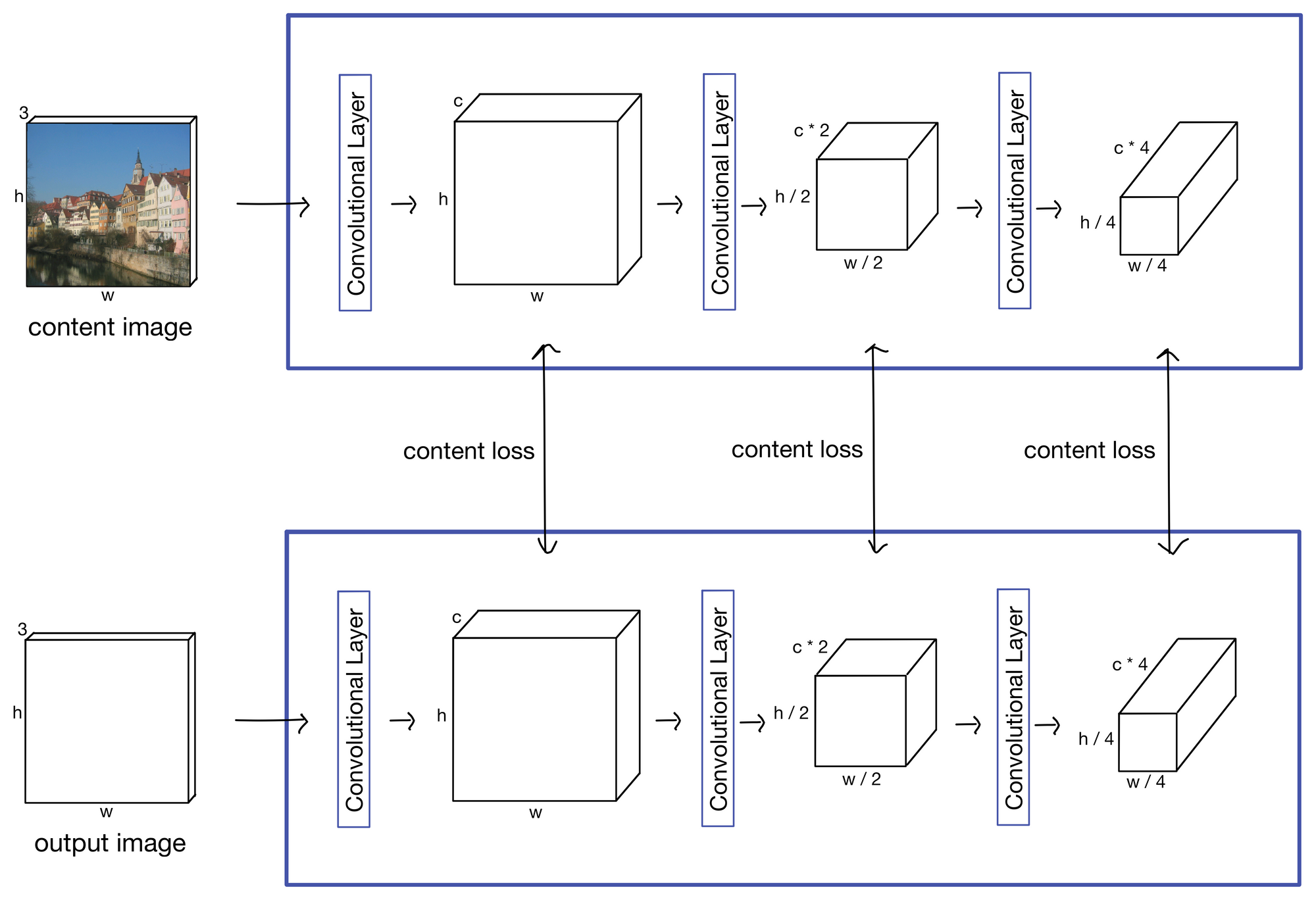
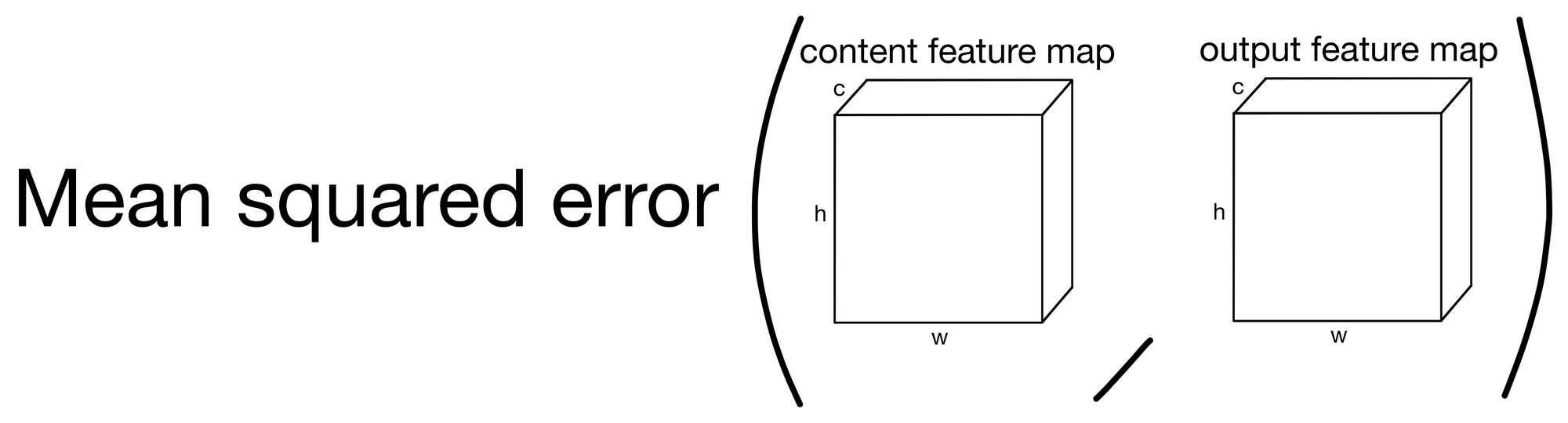
The content loss function itself is actually quite simple, simply the mean squared error (MSE) between the content feature maps and the stylized output feature maps. The MSE is taken for each pair of feature maps and summed to produce the final content loss for an iteration of network training.

Just a reminder that in my simplified network I show a loss component after each layer, but in actuality the feature maps used from VGG are those produced following a max pooling layer. Same goes for the style loss (shown next).

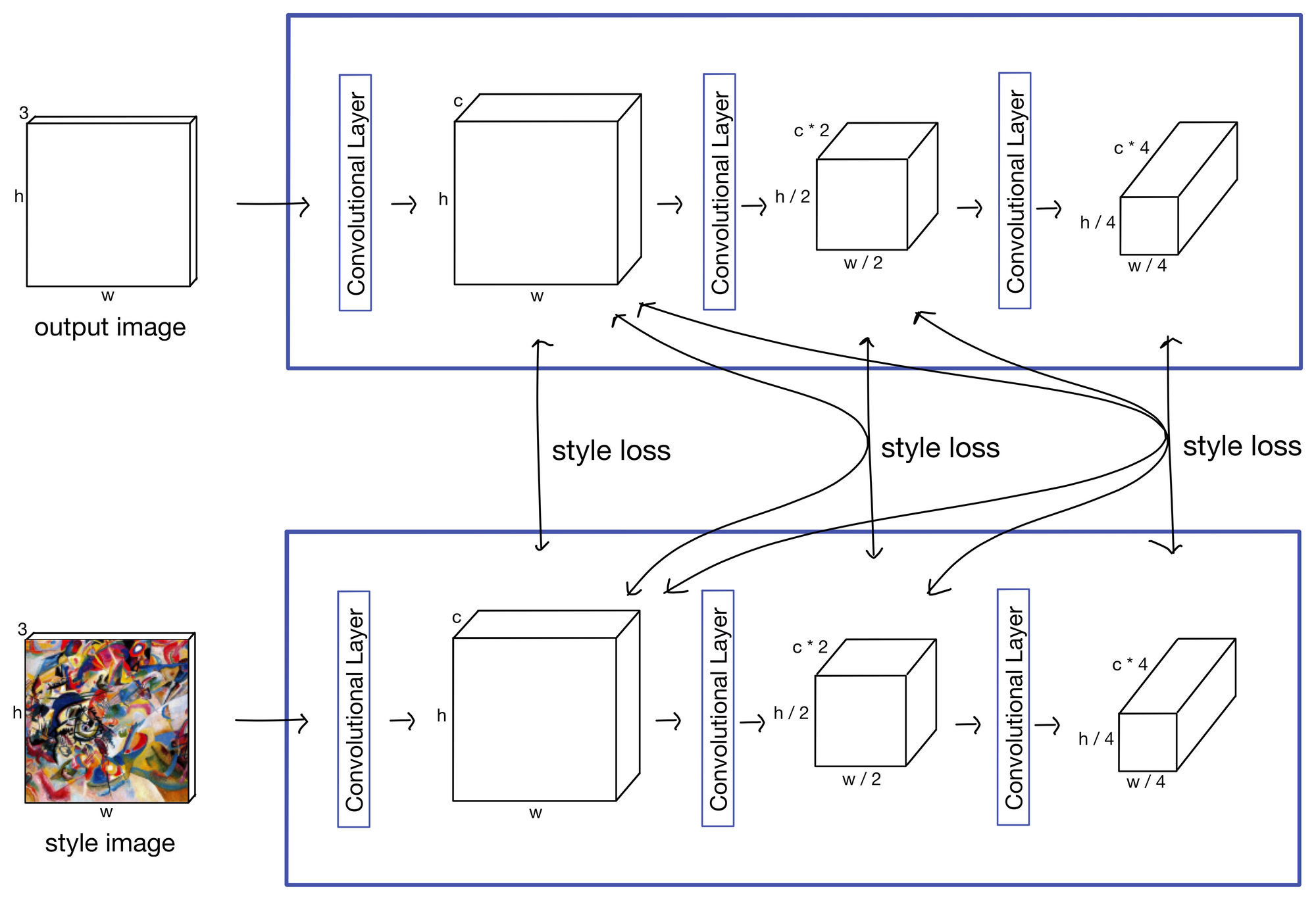
Style Loss

The second component of the loss function is the style loss. The style loss ensures the stylized image contains the style of the style image. Like content loss, style loss is also generated from the feature maps of each layer. However, instead considering each feature map separately, the feature maps are combined with feature maps from each proceeding layer.

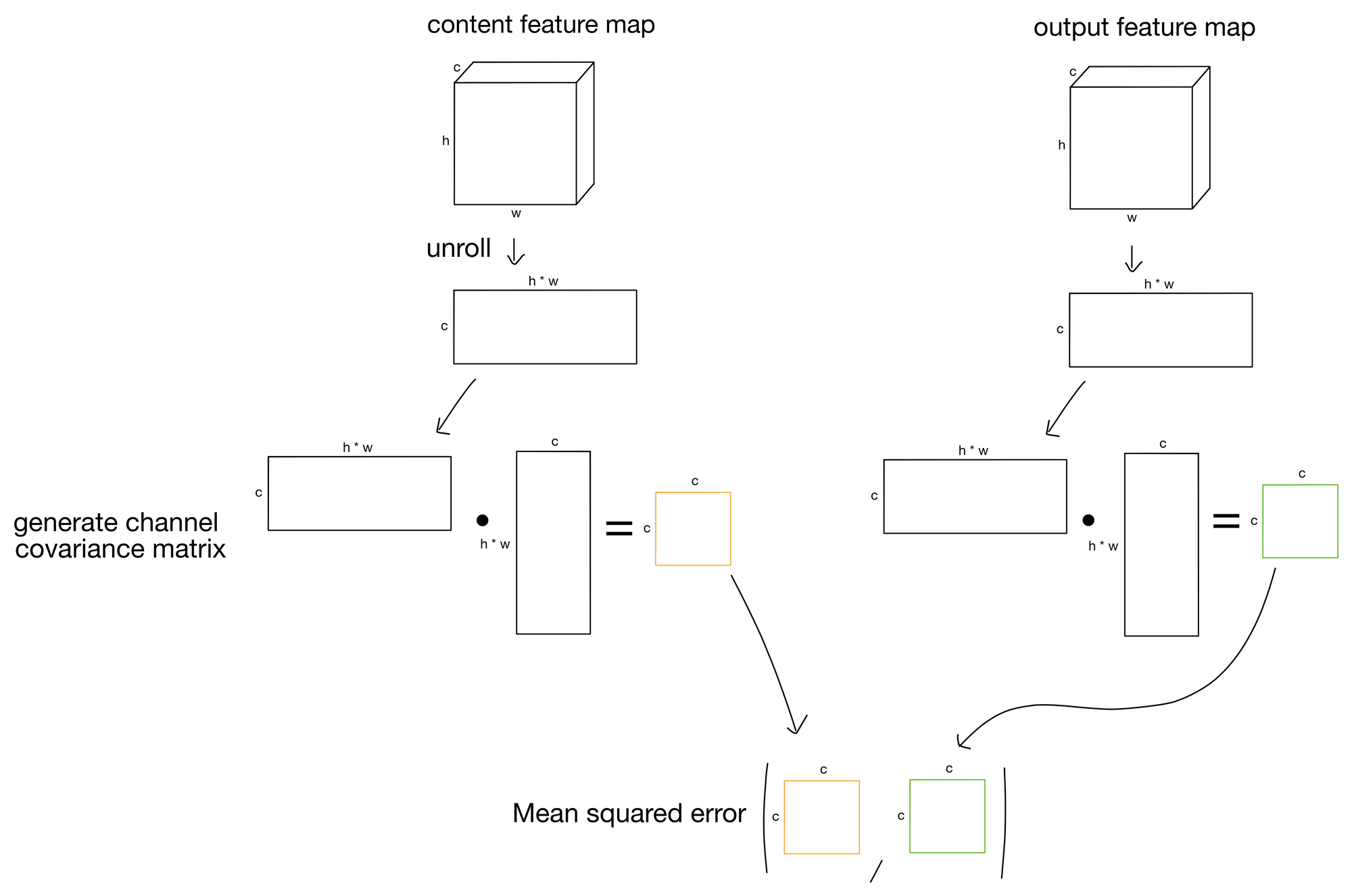
The style loss is calculated by taking the mean squared error of the gram matrices generated from the content and output feature maps (shown below). Here, the gram matrix describes the covariance of each feature map in the layer outputs. Conceptually, this operation ensures that the features produced by the content image and the stylized output image produce the same "flavor" of output. These "flavors" ultimately end up representing image style (which is kind of amazing if you ask me).

The network is then jointly optimized on both the style loss and content loss. The network also contains an extra hyperparameter that weights how much style vs. content is preserved in the stylized output image. After each training step the stylized output image contains more and more of the style of the style image and content of the content image.

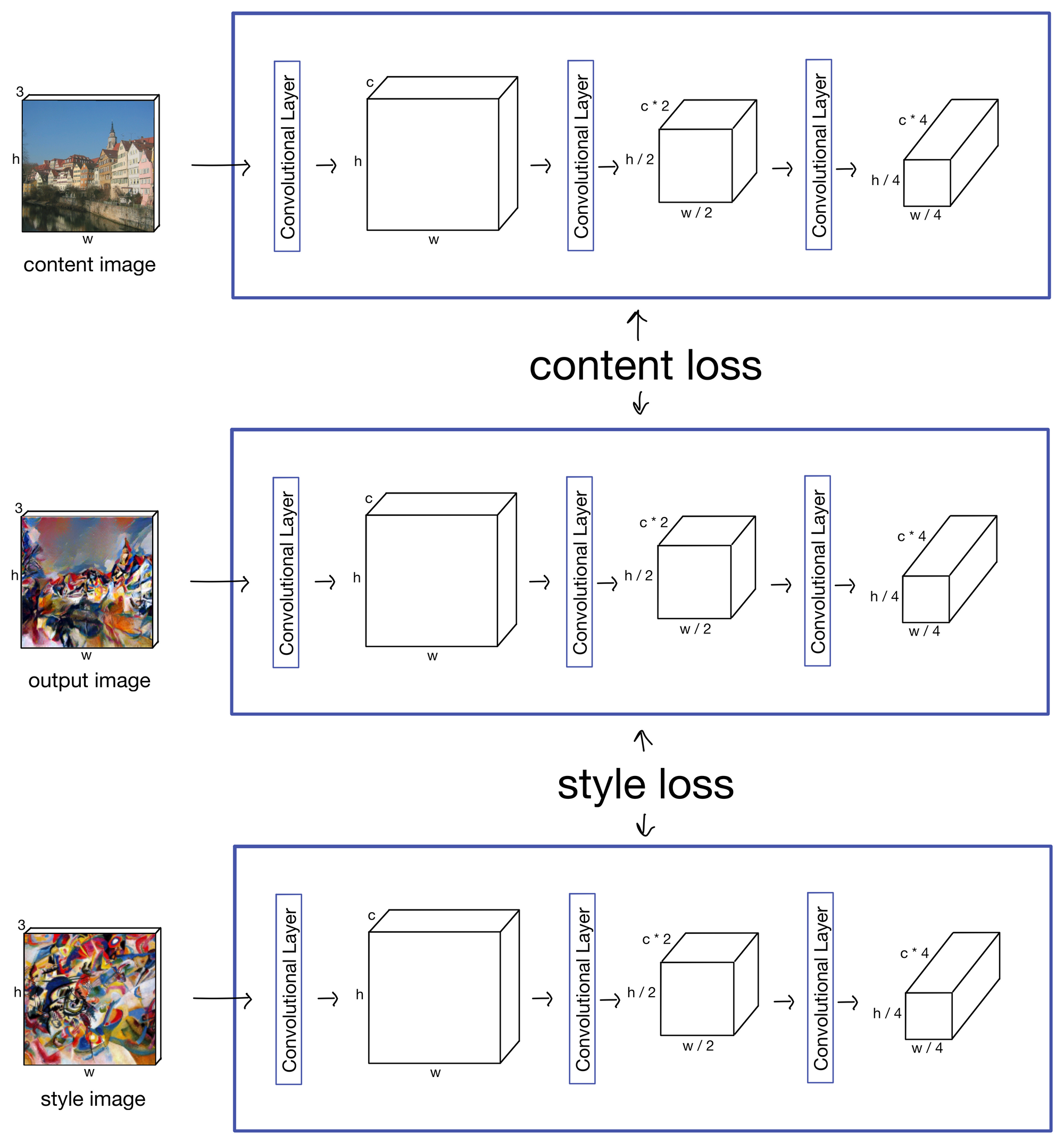
There you have it, one of the first networks for neural style transfer.

Cheers!

1. Gatys et al.: https://arxiv.org/abs/1508.06576
2. VGG: https://arxiv.org/abs/1409.1556