Paper Walkthrough - LongNet: Scaling Transformers to 1,000,000,000 Tokens

One of the biggest bottlenecks in Transformer models is the self-attention mechanism, which has a nasty quadratic computational cost with respect to the number of input tokens. For every token in the input, the model computes attention against every other token (n * n, where n is the sequence length), which becomes impossibly expensive for long sequences.

Sparse Attention

Sparse attention mechanisms aim to fix this by reducing the number of attention computations, thereby allowing each token to attend only to a subset of others, instead of all tokens. This works because not all token interactions are equally important, especially for long-range dependencies.

Various methods have been proposed, some are listed here:

• Sliding window attention: each token attends to a fixed local window (i.e. can only attend to neighbors)
• Strided attention: periodic sampling across the sequence, either random or fixed
• Learned sparsity: learned patterns of attention, i.e. which tokens attend to each other is learned by the model

But in this post, we focus on dilated attention, introduced by LongNet, introduced by Meta in 2023.

LongNet's Approach

LongNet avoids dense attention in two key ways:

• Splitting input tokens into w segments
• Selecting rows within each segment at fixed intervals (r)

More on those later. But first, lets refresh how standard attention is computed.

Vanilla Attention

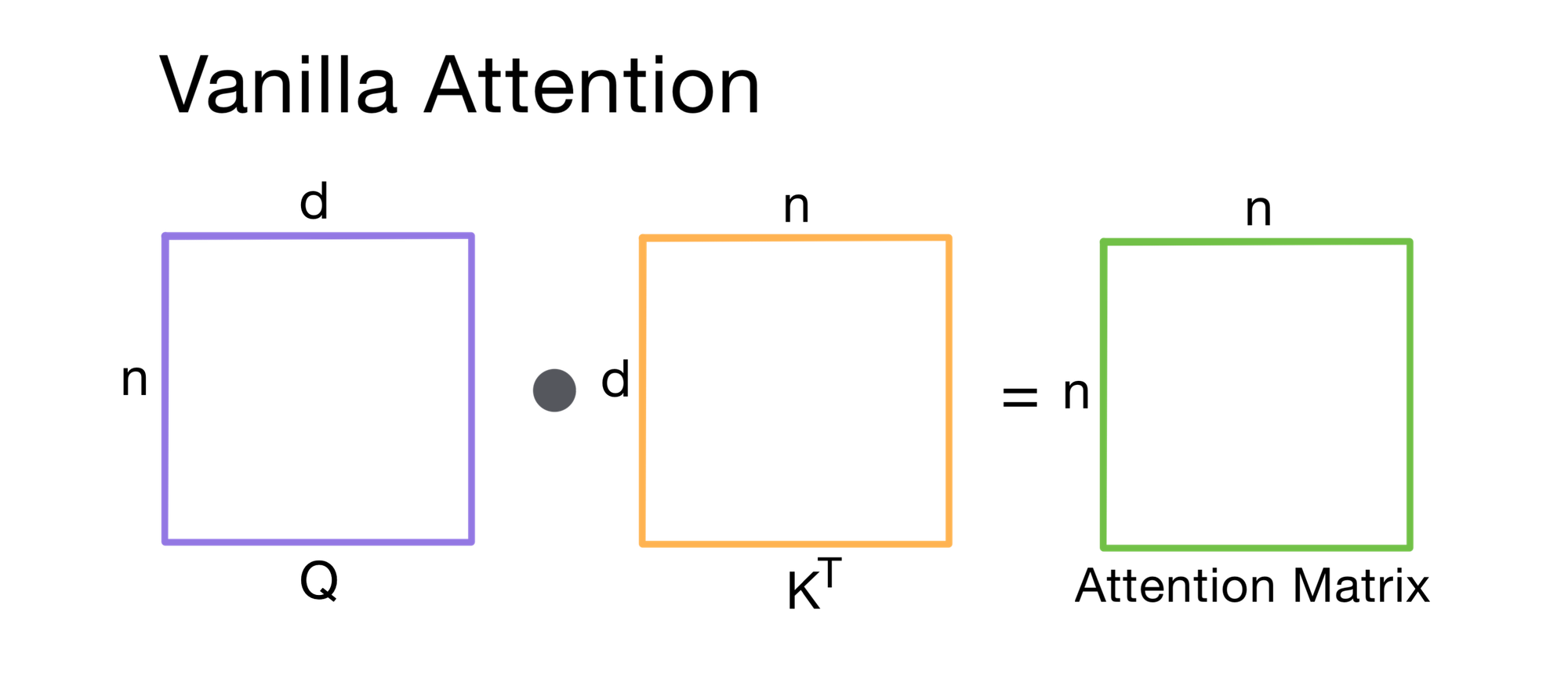
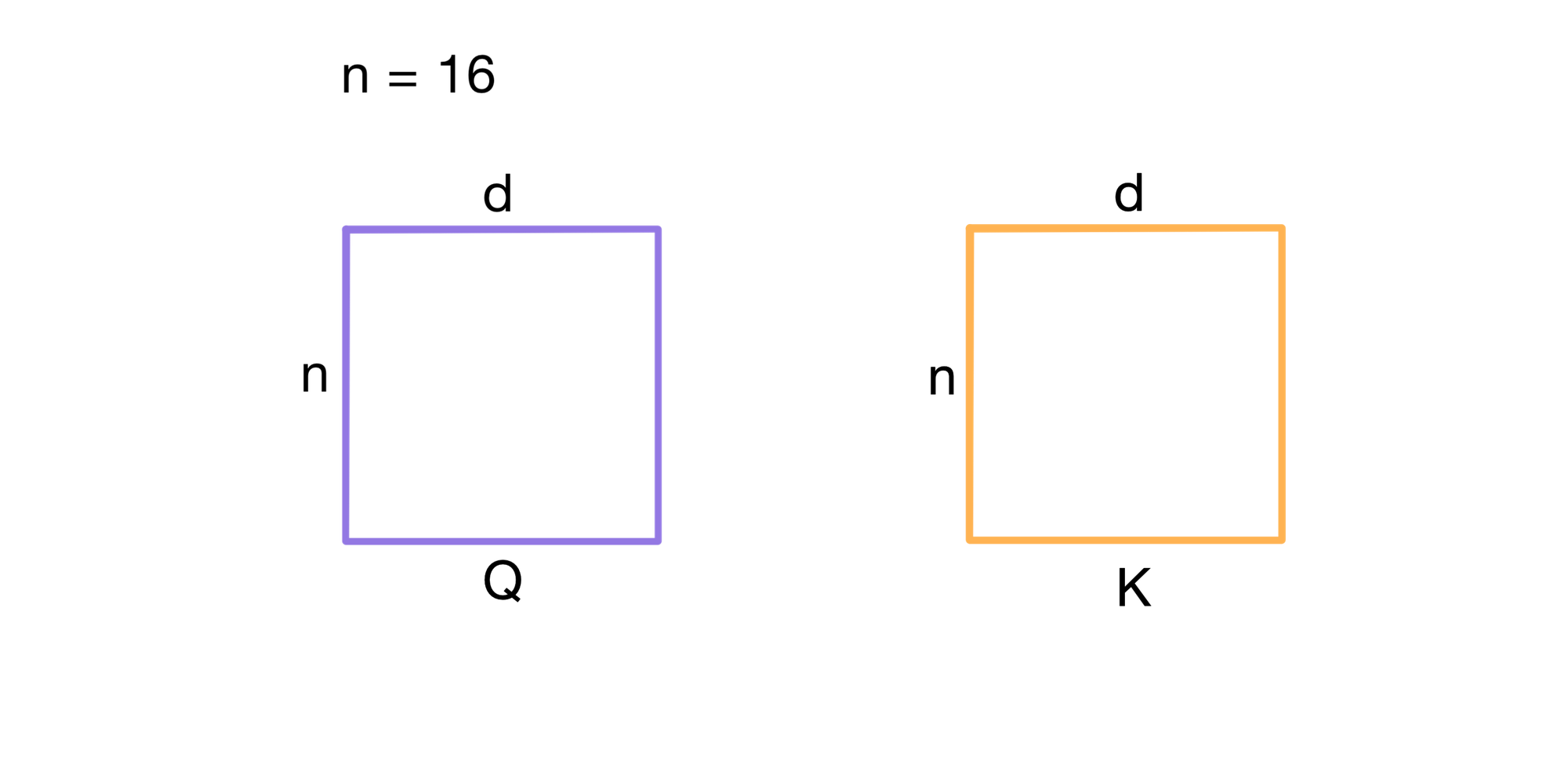
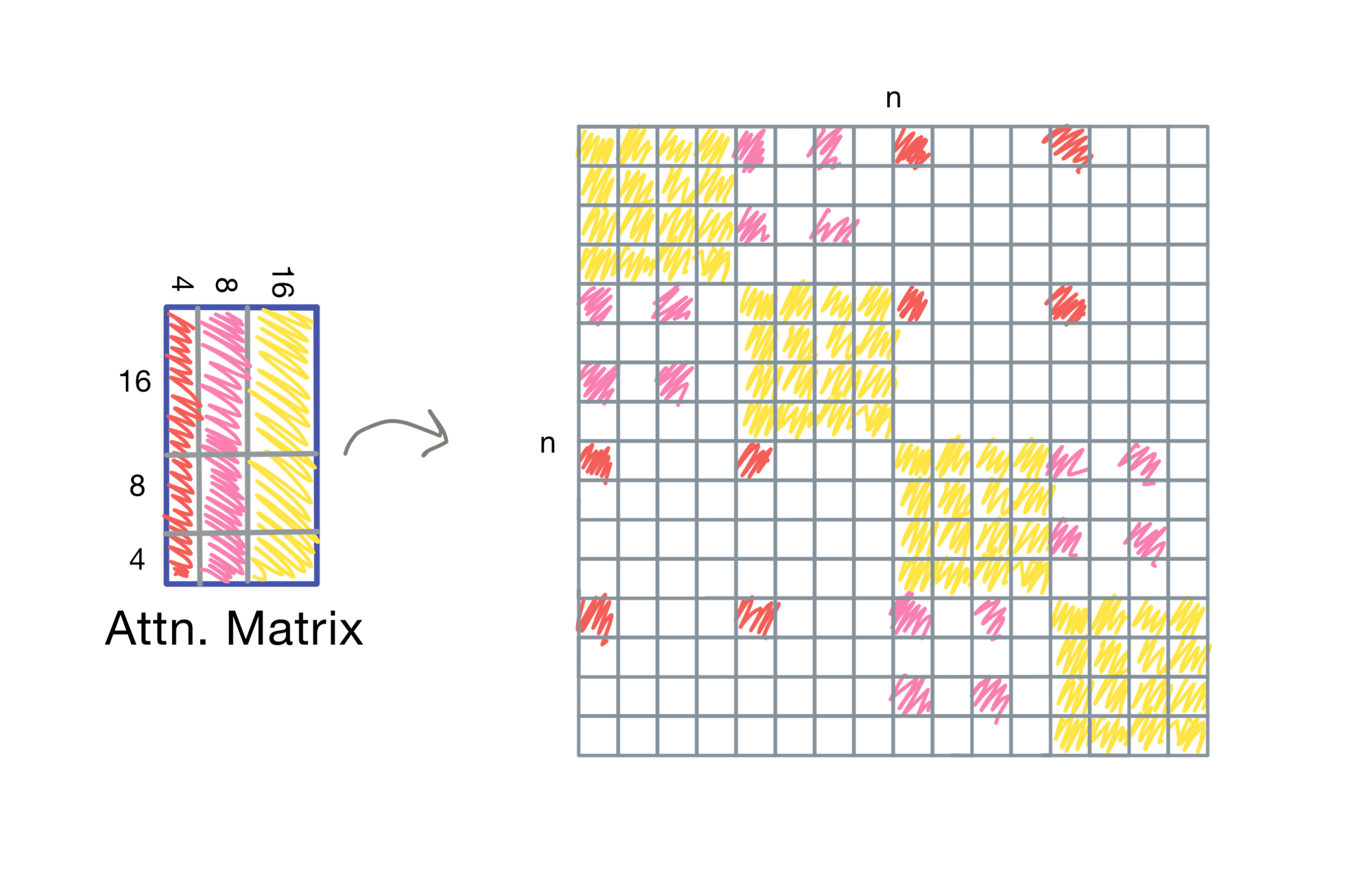
Let’s say we have a query matrix Q and key matrix K for a n=16 token input. In vanilla attention, the model computes a full dot-product between every query and every key, resulting in a dense 16 x 16 attention matrix.

Quadratic complexity, gross.

Dilated Attention

With dilated attention, LongNet sparsifies the attention matrix by selecting only some rows (at an interval r) within each segment (of size w). The process is the following:

1. Split the input sequence into equal-length chunks
2. Sparsify each chunk by selecting every rth token
3. Compute attention locally within each chunk
4. Scatter the result back into the full sequence

This process is repeated across different segment sizes and dilation rates to balance short- and long-range token dependencies

Prepping for Dilated Attention

To start, we prepare the query (Q), key (K), and value (V) matrices as follows:

• Q, K, and V are split into chunks on the sequence dimension
• Keys and values are sparsified and, in the case of K and V, gathered globally

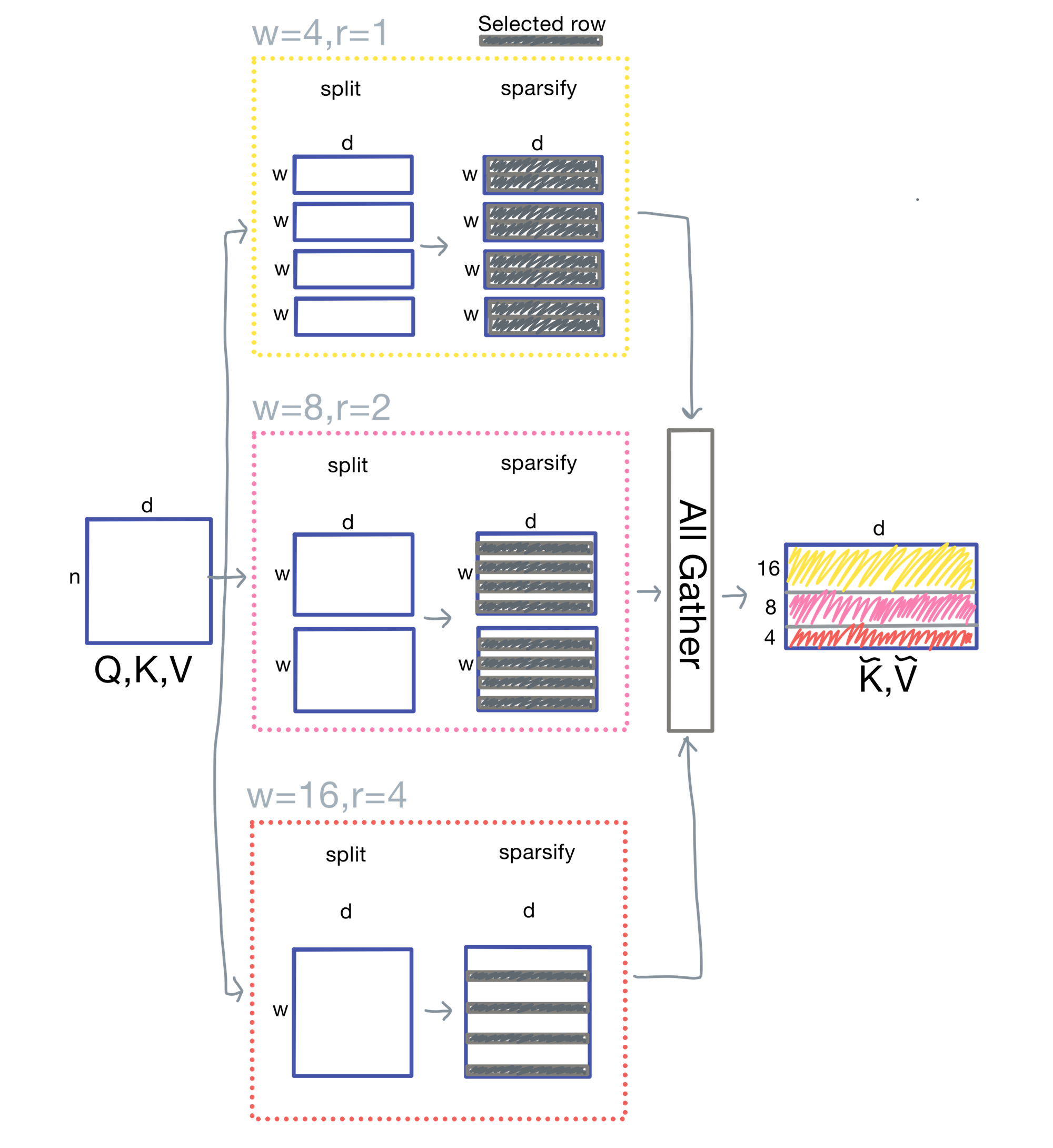
Note: Q is kept local; K and V are gathered across devices or attention blocks, crucial for keeping attention cost linear.

Generating the Dilated Attention Matrix

Once Q, K, and V are prepped:

• Each Q chunk is dotted with the gathered keys
• The results are collated into a sparse attention matrix
• Output tokens are then scattered back into the full sequence space

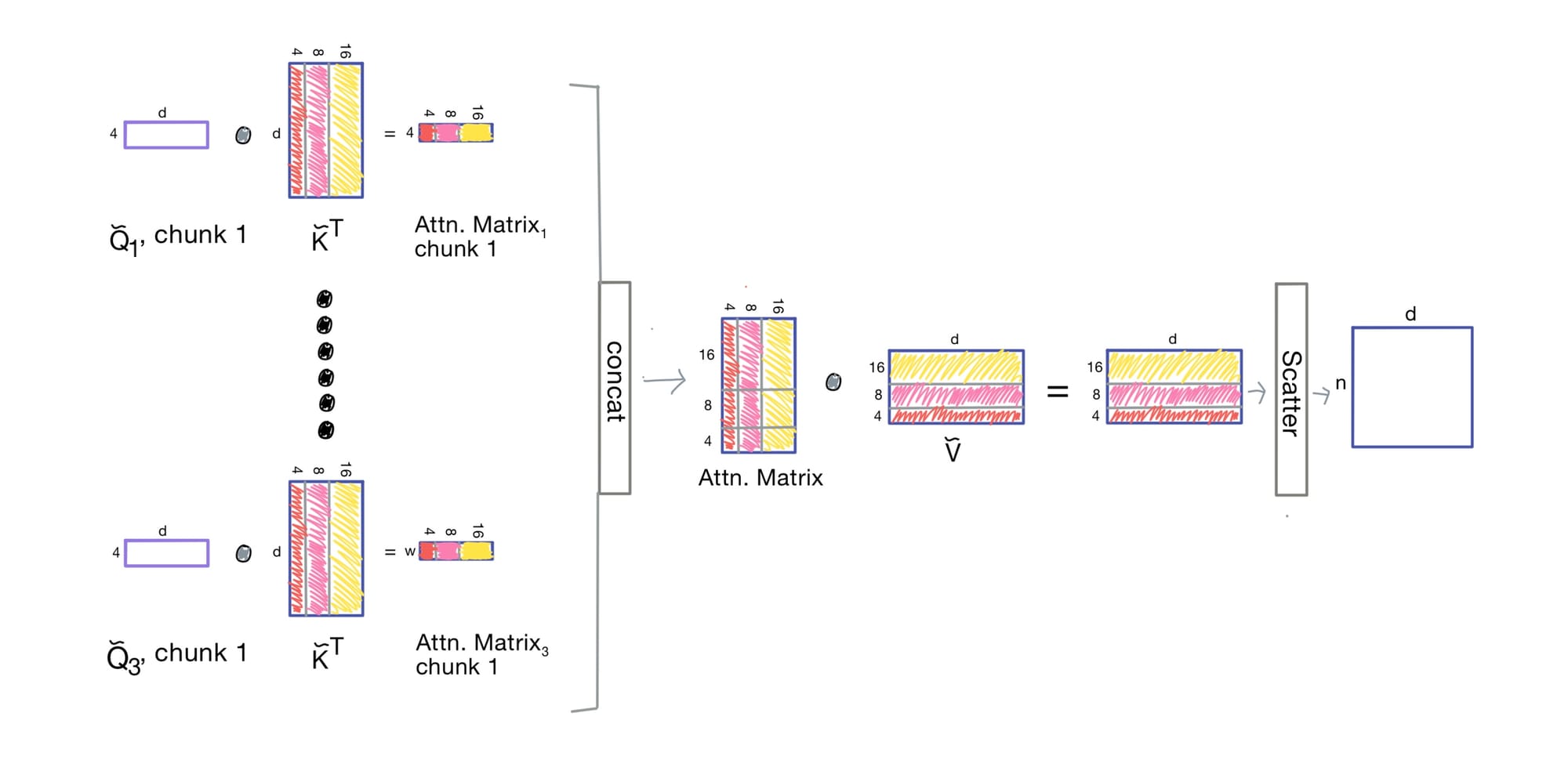
Compared to full attention, we use a fraction of the compute.

Visualizing Sparsity

Here we can visualize which portions of the attention matrix are actually used when comparing to regular attention. Note that if we were performing an autoregressive task, we would need to mask the result of the attention computation so tokens can not attend to tokens that come after them in the sequence.

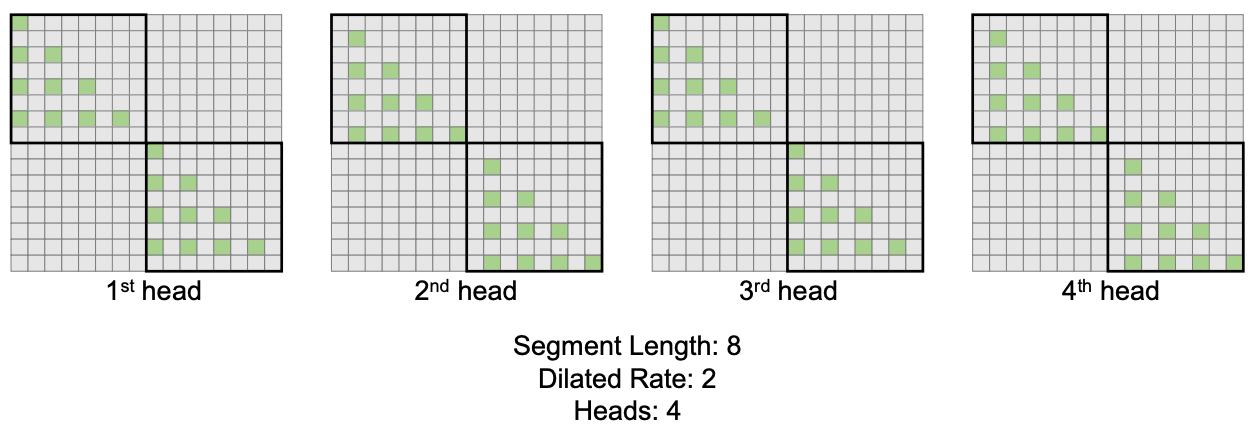
We can also stagger the heads if we are using multi-head attention each head is staggered with a different offset, so that the union of their attention covers a more diverse range of the input.

Parallelization Across GPUs

Most importantly, perhaps, dilated attention enables (relatively) easy parallelization, where each device (i.e. GPU) handles a different chunk of the sequence. And since keys and values are gathered globally, chunked queries can attend to tokens throughout the whole sequence via cross-attention.

This results in scalable training with linear time and memory growth, which is vital for foundation models. Speaking of which, my next post will be on GigaPath, a pathology image foundation model that uses dilated attention as one of it's key components.

This post is part one of a three part series that covers foundation models in image pathology. Check out the others here:

1. DINOv2
2. LongNet [this post!]
3. GigaPath [coming soon]